Тема 3. Електричні кола змінного струму
Тема №3. Електричні кола змінного струму
1. Поняття про змінний синусоїдальний струм.
2. Діючі і середні значення синусоїдальних ЕРС, струмів і напруг.
3. Зображення змінного
струму методом векторних діаграм
4. Резонансні явища в колах змінного струму
4.1. Послідовний ланцюг змінного струму з R, C, L. Резонанс напруг
4.2. Резонанс струмів. Умова резонансу струмів
5. Основні закони електротехніки в комплексному вигляді
6. Розрахунок електричних кіл комплексним(символічним ) методом
7. Активна, реактивна і повна потужності в колах змінного струму.4. Резонансні явища в колах змінного струму
4.1. Послідовний ланцюг змінного струму з R, C, L. Резонанс напруг
Розглянемо тепер ланцюг змінного струму, що містить індуктивність,
ємність
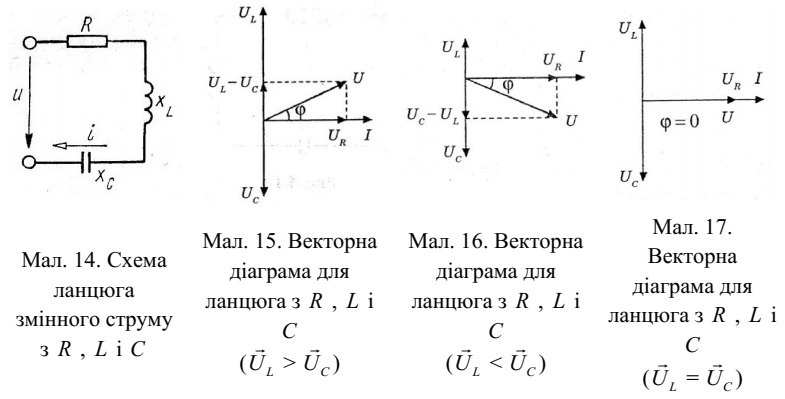
і резистор, включені послідовно (мал. 14).
Через усі елементи ланцюга
протікає той самий струм, тому в якості
основного виберемо вектор
струму й будемо будувати вектор напруги,
прикладеного до цього
ланцюга. Напруга, прикладене до ланцюга, дорівнює
векторній сумі падінь
напруг на котушці індуктивності, на ємності й на
резисторі:
![]()
Оскільки нам відомі
амплітуди й фази цих векторів, ми можемо побудувати векторну діаграму й знайти вектор Ù(мал. 15).
Із цієї векторної діаграми
ми можемо знайти модуль вектора
прикладеного до ланцюга
напруги Ù й зрушення по фазі ϕ між струмом і
напругою:
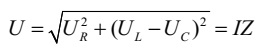
де величина
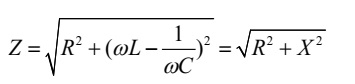
називається повним опором ланцюга. З векторної діаграми видно, що
зрушення по фазі між
струмом і напругою визначається рівнянням
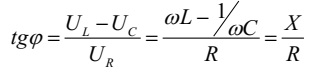
У результаті побудови діаграми ми одержали трикутник напруг,
гіпотенуза
якого дорівнює прикладеній напрузі Ù. При цьому різниця фаз між струмом і
напругою визначається співвідношенням векторів ÙL і ÙC. При ÙL> ÙC (див. мал. 15) кут ϕ позитивний і навантаження має індуктивний характер, при ÙL< ÙC кут ϕ негативний
і навантаження має ємнісний характер (мал. 16), а при ÙL= ÙC кут ϕ дорівнює
нулю й навантаження є чисто активним (мал.17).
Трикутнику напруг
відповідає трикутник опорів. Наприклад, для кола з
активним і індуктивним
опорами ( X L > X C або X C = 0, мал. 18) і кола
з
активним і ємнісним опором
( X C > X L або X L = 0, мал. 19).

Резонансом
напруг називають явище в
ланцюзі з послідовним контуром,
коли струм у ланцюзі
збігається по фазі з напругою джерела.
Знайдемо умову резонансу
напруг. Для того щоб струм ланцюга збігався
по фазі з напругою,
реактивний опір повинний бути дорівнює нулю, тому що

При резонансі
напруг частота джерела дорівнює власній частоті коливань
контуру.
Вираз (24) є формулою Томсона, що визначає залежність власної частоти коливань контуру f0 від параметрів L і C .