Тема 3. Електричні кола змінного струму
| Site: | Освітній сайт КНУБА |
| Course: | Основи електротехніки та електроніки (Ковал) |
| Book: | Тема 3. Електричні кола змінного струму |
| Printed by: | Гість-користувач |
| Date: | Tuesday, 3 March 2026, 2:02 PM |
Description
Тема №3. Електричні кола змінного струму
1. Поняття про змінний синусоїдальний струм.
2. Діючі і середні значення синусоїдальних ЕРС, струмів і напруг.
3. Зображення змінного
струму методом векторних діаграм
4. Резонансні явища в колах змінного струму
4.1. Послідовний ланцюг змінного струму з R, C, L. Резонанс напруг
4.2. Резонанс струмів. Умова резонансу струмів
5. Основні закони електротехніки в комплексному вигляді
6. Розрахунок електричних кіл комплексним(символічним ) методом
7. Активна, реактивна і повна потужності в колах змінного струму.Table of contents
- 1. Поняття про змінний синусоїдальний струм
- 2. Діючі і середні значення синусоїдальних ЕРС, струмів і напруг
- 3. Зображення змінного струму методом векторних діаграм
- 4. Резонансні явища в колах змінного струму
- 5. Основні закони електротехніки в комплексному вигляді
- 6. Розрахунок електричних кіл комплексним(символічним ) методом
- 7. Активна, реактивна і повна потужності в колах змінного струму
1. Поняття про змінний синусоїдальний струм
Змінним
називають
струм, зміна якого за значенням і напрямком
повторюється періодично через рівні проміжки часу.
Широке застосування змінного струму в різних областях техніки
пояснюється легкістю його одержання й перетворення, а
також простотою
устрою генераторів і двигунів змінного струму,
надійністю їх роботи й
зручністю експлуатації.
Розглянемо принцип дії найпростішого генератора
змінного струму.
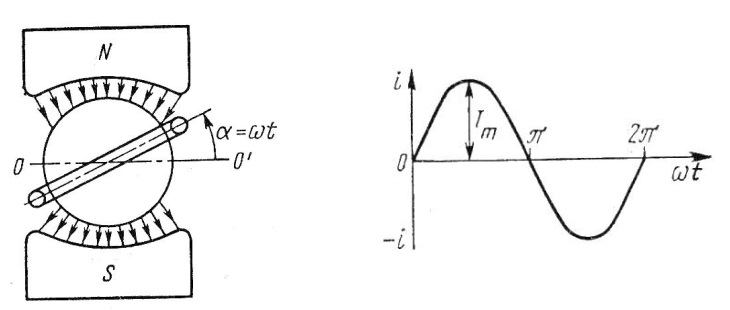
|
Мал. 1. Модель генератора |
Мал. 2. Графік синусоїдального струму |
Між полюсами електромагніту або постійного магніту (мал. 1) в
одноріднім
магнітнім полі рівномірно обертається з кутовою швидкістю ω
рамка
площею S .
Магнітний потік через
рамку
![]()
Величину ω також називають круговою частотою.Через те що при обертанні рамки магнітний потік, що її перетинає,
увесь час
міняється, то за законом електромагнітної індукції в ній буде ЕРС індукції
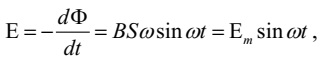
де
Ε m = BSω -
амплітуда (максимальне значення) синусоїдальної ЭДС, що
виникає в рамці.
Якщо до затискачів
генератора підключити навантаження, то через неї
піде струм, який також
буде змінюватися за синусоїдальним законом. Графік
синусоїдального струму i = I m sinωt представлений на мал. 2. По осі ординат
відкладають струм i , по осі абсцис -
кут α = ω t або час t .
Значення e = E (t) змінної ЭДС (а також струму й напруги) у поточний
момент часу називається миттєвим значенням.
Величину 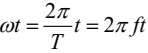 ,
що стоїть під знаком синуса або косинуса,
,
що стоїть під знаком синуса або косинуса,
називають фазою коливань,
описуваних цими функціями. Фаза визначає
значення ЕРС у будь-який
момент часу t й виміряється в градусах або радіанах.
Величина f називається частотою коливань
і пов'язана із круговою частотою співвідношенням ω = 2πf .
Час T однієї повної зміни
ЕРС (час одного оберту рамки) називають
періодом ЕРС. Зміна напруги, струму й ЕРС з часом може бути зображена на
часовій діаграмі (мал. 3).
Частота коливань пов'язана
з періодом співвідношенням f= 1/T. Якщо
період виміряється в
секундах, то частота - у герцах (Гц). У більшості країн,
включаючи Україну,
промислова частота змінного струму становить 50 Гц (у
США і Японії - 60 Гц).
Величина промислової
частоти змінного струму обумовлена техніко
економічними міркуваннями.
Якщо вона занадто низка, то збільшуються
габарити електричних машин
і, отже, витрата матеріалів на їхнє виготовлення; помітним стає
миготіння світла в електричних лампочках. При занадто високих частотах
збільшуються втрати енергії, пов'язані з перемагнічуванням сердечників електричних
машин і трансформаторах. Тому найбільш оптимальними виявилися частоти 50-60 Гц. Однак у деяких випадках використовуються
змінні струми як з більш високої, так і з більш низькою частотою. Наприклад, у
літаках застосовується частота 400 Гц. На цій частоті можна значно зменшити
габарити й вагу трансформаторів і електромоторів, що для авіації більш суттєво,
ніж збільшення втрат у сердечниках. На залізницях використовують змінний
струм із частотою 25 Гц і навіть 16,66 Гц.
2. Діючі і середні значення синусоїдальних ЕРС, струмів і напруг
Для опису роботи змінного струму миттєві значення незастосовні, а
середні
значення за період дорівнюють нулю. Тому
вводять поняття діючих
значень струму й напруги,
які засновані на тепловій дії струму, що не залежить від його напрямку.
Діючими
значеннями струму й
напруги називають відповідні параметри
такого постійного
струму, при якім у даному провіднику за даний проміжок
часу виділяється
стільки ж теплоти, що й при змінному.
Таким чином, діюче
значення змінного струму рівно такому постійному
струму, який за час,
рівний одному періоду, виділяє на даному резисторі
однакову кількість теплоти
зі змінним струмом.
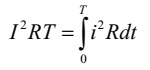
Скоротивши на
загальний множник R і врахувавши, що i = I m sinωt,
знайдемо вираз для діючого
значення струму:

Діючі значення
позначаються прописними латинськими буквами без
індексів.
Електровимірювальні
прилади змінного струму проградуйовані в діючих
значеннях вимірюваних
величин. Іноді діючі значення називають ефективними.
3. Зображення змінного струму методом векторних діаграм
Метод векторних діаграм, тобто зображення величин, що
характеризують змінний
струм векторами, а не тригонометричними функціями, надзвичайно зручний. Тому коротко викладемо його основи.
Змінний струм на відміну
від постійного характеризується двома
скалярними величинами -
амплітудою й фазою. Тому для математичного опису змінного струму необхідний математичний об'єкт, що також
характеризується двома скалярними
величинами. Існують два такі математичні об'єкти (з відомих нам) - вектор на площині й комплексне число. У теорії електричних
кіл і ті й інші
використовуються для опису змінних струмів.
При описі електричного
ланцюга змінного струму за допомогою векторних діаграм кожному струму й напрузі зіставляється вектор на
площині в
полярних координатах, довжина якого
дорівнює амплітуді
струму або
напруги, а полярний кут -
відповідний до фази.
Нехай заданий
синусоїдальний струм
i = I m sin(ωt+ ψ) .
Графік цього струму має
вигляд синусоїди, зображеної на мал. 4. Поруч
зображений вектор, що
відповідає побудованій синусоїді. Цей вектор із
модулем, що дорівнює
амплітуді, нахилений до горизонтальної осі під кутом ψ.
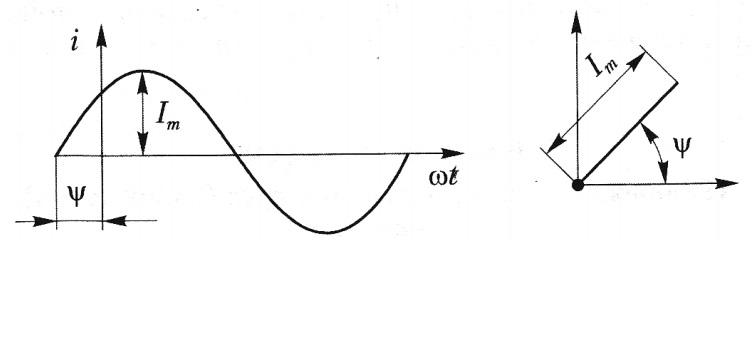
Мал. 4. Графік синусоїдального струму і його векторна діаграма
Оскільки
фаза змінного струму залежить від часу, уважається, що всі
вектори
обертаються проти годинникової стрілки із частотою змінного струму.
Векторна діаграма
будується для фіксованого моменту часу.
Більш докладна побудова й
використання векторних діаграм буде викладена нижче на прикладах конкретних ланцюгів.
4. Резонансні явища в колах змінного струму
4.1. Послідовний ланцюг змінного струму з R, C, L. Резонанс напруг
4.2. Резонанс струмів. Умова резонансу струмів
4.1. Послідовний ланцюг змінного струму з R, C, L. Резонанс напруг
Розглянемо тепер ланцюг змінного струму, що містить індуктивність,
ємність
і резистор, включені послідовно (мал. 14).
Через усі елементи ланцюга
протікає той самий струм, тому в якості
основного виберемо вектор
струму й будемо будувати вектор напруги,
прикладеного до цього
ланцюга. Напруга, прикладене до ланцюга, дорівнює
векторній сумі падінь
напруг на котушці індуктивності, на ємності й на
резисторі:
![]()
Оскільки нам відомі
амплітуди й фази цих векторів, ми можемо побудувати векторну діаграму й знайти вектор Ù(мал. 15).
Із цієї векторної діаграми
ми можемо знайти модуль вектора
прикладеного до ланцюга
напруги Ù й зрушення по фазі ϕ між струмом і
напругою:
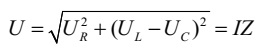
де величина
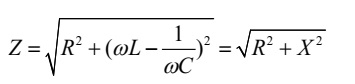
називається повним опором ланцюга. З векторної діаграми видно, що
зрушення по фазі між
струмом і напругою визначається рівнянням
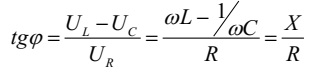
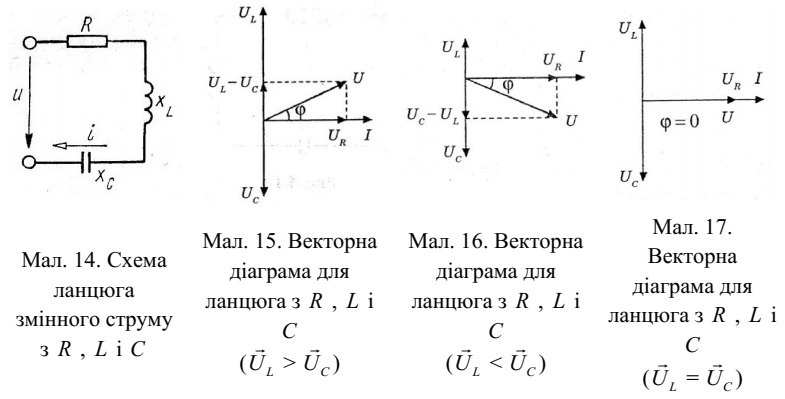
У результаті побудови діаграми ми одержали трикутник напруг,
гіпотенуза
якого дорівнює прикладеній напрузі Ù. При цьому різниця фаз між струмом і
напругою визначається співвідношенням векторів ÙL і ÙC. При ÙL> ÙC (див. мал. 15) кут ϕ позитивний і навантаження має індуктивний характер, при ÙL< ÙC кут ϕ негативний
і навантаження має ємнісний характер (мал. 16), а при ÙL= ÙC кут ϕ дорівнює
нулю й навантаження є чисто активним (мал.17).
Трикутнику напруг
відповідає трикутник опорів. Наприклад, для кола з
активним і індуктивним
опорами ( X L > X C або X C = 0, мал. 18) і кола
з
активним і ємнісним опором
( X C > X L або X L = 0, мал. 19).

Резонансом
напруг називають явище в
ланцюзі з послідовним контуром,
коли струм у ланцюзі
збігається по фазі з напругою джерела.
Знайдемо умову резонансу
напруг. Для того щоб струм ланцюга збігався
по фазі з напругою,
реактивний опір повинний бути дорівнює нулю, тому що

При резонансі
напруг частота джерела дорівнює власній частоті коливань
контуру.
Вираз (24) є формулою Томсона, що визначає залежність власної частоти коливань контуру f0 від параметрів L і C .
4.2. Резонанс струмів. Умова резонансу струмів
Таким чином, резонанс струмів - це режим кола змінного струму з паралельними індуктивністю та ємністю, при якому струм у нерозгалуженій частині кола і напруга прикладена до кола збігаються за фазою. Тому його ще називають фазовий резонанс. При резонансі струмів струми у паралельних гілках можуть бути набагато більшими за струм від джерела, але вони взаємно врівноважуються і тому не впливають на загальний струм.
Умова виникнення
резонансу струмів: ![]()
Повний опір кола при резонансі струмів по відношенню до джерела (резонансний опір):
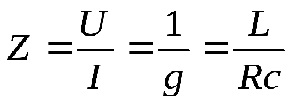
Тобто, чим менше активний опір, тим більше резонансний опір кола. Коли активний опір дорівнює нулю, резонансний опір прагне до нескінченості і струм у нерозгалуженій ділянці кола дорівнює нулю.
Повна провідність кола при резонансі дорівнює активній провідності кола:
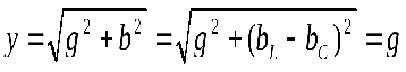 , так як
, так як ![]()
Характерний опір кола:
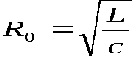
Добротністю контуру називають відношення характерного опору кола до його активного опору:
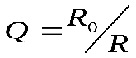 або
або ![]()
Вона характеризує кратність індуктивного струму до струму у нерозгалуженій ділянці кола.
Якщо контур має активні втрати енергії, то коливання у ньому згасають з часом. Згасання контуру - це величина, яка обернена добротності:
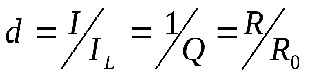
Вона показує яку частину струму контуру складає струм у нерозгалуженій ділянці кола при резонансі струмів.
Резонансна кутова частота при нехтуванні активними опорами котушки і конденсатора :
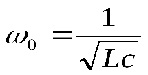
Якщо врахувати активні опори котушки і конденсатора, то:
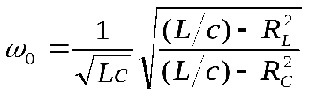
При резонансі струмів реактивні потужності індуктивності і ємності однакові, тому повна реактивна буде дорівнювати нулю:
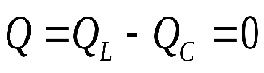
Від джерела живлення до кола поступає лише активна енергія: S=P
При дослідженні
резонансних явищ велику роль грають резонансні криві - залежність діючого
значення струму від частоти прикладеної напруги: ![]() - (рис.15.3.) Резонанс струмів використовують
в радіотехніці, пристроях автоматики, телемеханіки і зв’язку. З іншого боку,
виникнення режимів близьких до резонансу, але в не передбачених для цього
пристроях, може привести до порушення його нормальної роботи чи аварії.
- (рис.15.3.) Резонанс струмів використовують
в радіотехніці, пристроях автоматики, телемеханіки і зв’язку. З іншого боку,
виникнення режимів близьких до резонансу, але в не передбачених для цього
пристроях, може привести до порушення його нормальної роботи чи аварії.
Резонанс струмів може виникнути і в розгалуженому колі, яке має кілька гілок з R, L, c, якщо реактивна провідність всього кола дорівнює нулю:
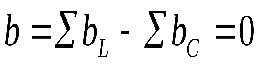
Залежність опору від частоти вказана на рисунку 15.3.
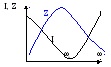
Рисунок 15.3 - Резонансні криві
5. Основні закони електротехніки в комплексному вигляді
Вводячи комплекси повного опору, діючих значень струму і напруг отримуємо закон Ома у комплексній формі: комплексний струм на ділянці кола прямо пропорційний комплексній напрузі на її затискачах і обернено пропорційний комплексу повного опору ділянки:
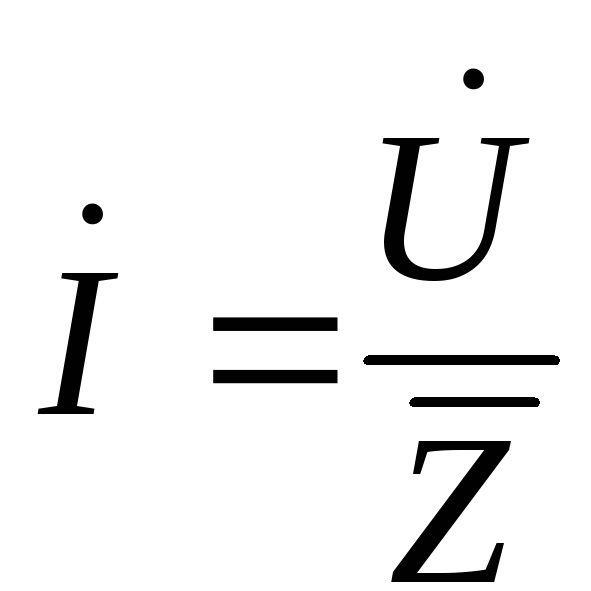 , де
, де ![]()
Комплекс еквівалентного опора послідовного сполучення дорівнює сумі окремих комплексів опорів:
![]()
Комплекс еквівалентного опора паралельного сполучення дорівнює :
![]()
Комплекс еквівалентної провідності паралельного сполучення дорівнює сумі окремих комплексів провідностей:
![]()
І закон Кірхгофа у комплексній формі: алгебраїчна сума комплексних струмів у вузлі дорівнює нулю:
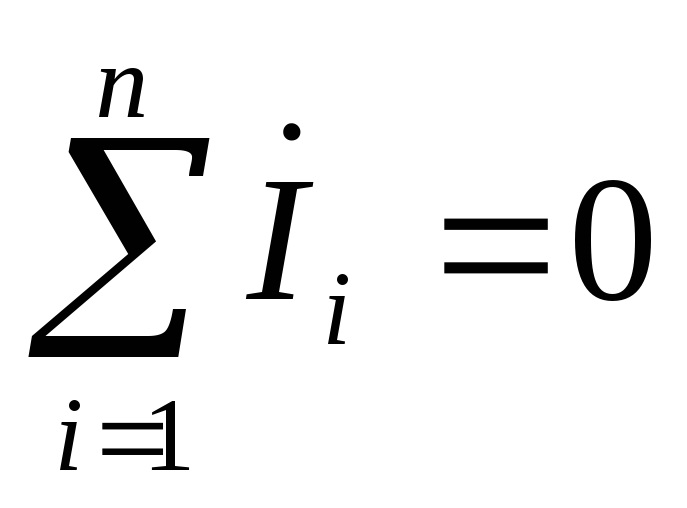
При цьому комплекси струмів, які входять до вузла, вважають позитивними, а комплекси струмів, які виходять з вузла, вважають негативними.
ІІ закон Кірхгофа у комплексній формі: алгебраїчна сума комплексів падінь напруги на ділянках контуру дорівнює алгебраїчній сумі комплексів ЕРС, діючих у контурі:
![]()
Для написання рівняння за другим законом Кірхгофа потрібно обрати напрямок обходу контуру та напрямки струмів і ЕРС довільно. Якщо обхід контуру збігається з напрямком ЕРС чи струмом, то їх комплекси враховують зі знаком «+» і навпаки.
Символічний метод дозволяє використовувати для розрахунку кіл змінного струму усі методи розрахунку кіл постійного струму: метод згортання, перетворення зірки в трикутник і навпаки, законів Кірхгофа, вузлових потенціалів, контурних струмів, еквівалентного генератора і накладання, але для розрахунків у цьому випадку використовують комплекси змінних величин.
6. Розрахунок електричних кіл комплексним(символічним ) методом
При зміні параметра кола
(активного опору, ємності чи індуктивності) для струмів і напруг на окремих
ділянках кола будуть різні значення. Проаналізувати зміну режимів кола можна
побудовою серії векторних діаграм. Кругові діаграми - це серії векторних діаграм
при зміні параметрів кола. Їх використовують для визначення струму чи напруги
при певному значенні параметру, який змінюється (активного опору, ємності чи
індуктивності). Наприклад, визначати значення струму при активному опорі, який
дорівнює ![]() , для вказаного на ( рис.17.3) кола. Активний
опір можна змінювати. До цього кола подається синусоїдна напруга:
, для вказаного на ( рис.17.3) кола. Активний
опір можна змінювати. До цього кола подається синусоїдна напруга:![]()
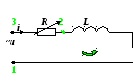
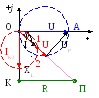
Рисунок 17.3 - Нерозгалужене коло зі змінним активним опором і його кругові діаграми
Рисунок 17.4- Топографічна діаграма кола вказаного на рис.17.3
Побудуємо кругові діаграми (рис.17.3).
Відкладаємо вектор
комплексу напруги: ![]()
При R=0 спостерігається
коротке замкнення. При цьому режимі струм у колі найбільш можливий:![]() , і відстає від напруги на кут 90º. Показуємо
це на діаграмі і проводимо окружність з діаметром
, і відстає від напруги на кут 90º. Показуємо
це на діаграмі і проводимо окружність з діаметром![]() . Уздовж вектора
. Уздовж вектора![]() відкладаємо відрізокОК, який у
масштабі дорівнює . З точкиК проведемо
перпендикуляр цьому вектору - відрізок КП, який у масштабі
дорівнює
відкладаємо відрізокОК, який у
масштабі дорівнює . З точкиК проведемо
перпендикуляр цьому вектору - відрізок КП, який у масштабі
дорівнює ![]() , при якому струм у колі зменшується:
, при якому струм у колі зменшується:![]() . Якщо з’єднати прямою лінією точкиО і П отримаємо
точки 1 і 2 на кругових
діаграмах, які і визначать режим роботи при заданому активному опорі
. Якщо з’єднати прямою лінією точкиО і П отримаємо
точки 1 і 2 на кругових
діаграмах, які і визначать режим роботи при заданому активному опорі ![]() : діюче значення струму - відрізокО1,
який нахилений під кутом φ до вектора напруги, активна складова прикладеної до
кола напруги - відрізок О2, реактивна складова прикладеної до кола
напруги - відрізокОА.
: діюче значення струму - відрізокО1,
який нахилений під кутом φ до вектора напруги, активна складова прикладеної до
кола напруги - відрізок О2, реактивна складова прикладеної до кола
напруги - відрізокОА.
Напруга між двома точками електричного кола уявляє собою різницю потенціалів цих точок. Тобто, потенціал окремої точки можна представити відповідним комплексом потенціалу і зобразити вектором, який починається у початку координат. Його кінець позначають той же цифрою або буквою, що і точку кола, потенціал якої зображає вектор.
Топографічною діаграмою називається векторна діаграма комплексів кола при умові, що кожній точці кола відповідає певна точка на діаграмі і вектор, проведений з початку координат в будь-яку точку діаграми, зображає комплекс потенціалу цієї точки. В цьому випадку відрізок, який з’єднує дві будь-які точки діаграми, визначає комплекс напруги між цими точками.
При побудові топографічної діаграми потенціал будь-якої точки приймають рівним нулю і на діаграмі точку нульового потенціалу суміщають з початком координат.
7. Активна, реактивна і повна потужності в колах змінного струму
Інтенсивність
процесів одержання, передачі, перетворення й споживання
електричної енергії
визначає потужність. Залежно від характеру процесів, що відбуваються в ланцюгах змінного струму, розрізняють активну,
реактивну та повну потужність.
Активна потужність P характеризує
величину споживаним ланцюгом
енергії, що не вертається
джерелу живлення, тобто енергії, що переходить
безповоротно з електричної
в інші види – наприклад, теплоту або механічну
роботу.
Реактивна
потужність визначає
інтенсивність обміну електричною
енергією між джерелом і
реактивним навантаженням.
Повна потужність визначає вимоги, пропоновані до джерела живлення,
його габарити й вартість.
Джерело повинно бути розраховане на споживані
ланцюгом струм і напругу,
незалежно від величини активної потужності. Ця
величина вказується на
табличках приладів змінного струму.
Повна потужність і її
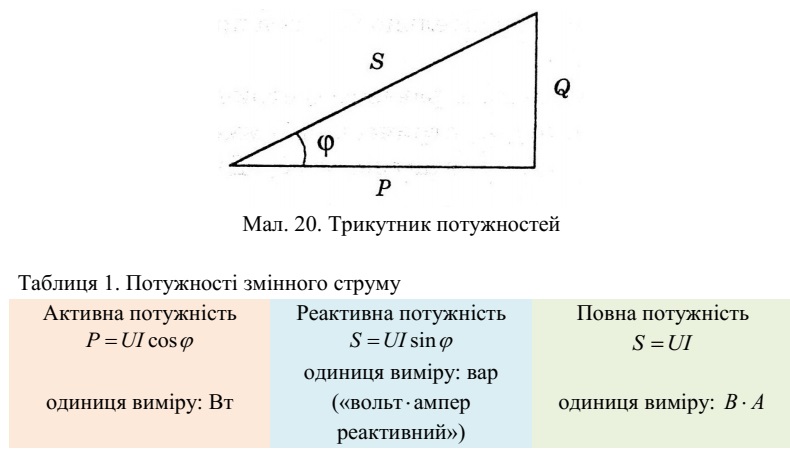
складові зв'язані між собою співвідношенням
S2 = P2
+ Q2 (25)
і можуть бути представлені
трикутником потужностей, який подібний до
трикутників напруг і
опорів (мал. 20).
Активна (корисна)
потужність P залежить від струму, напруги й cosϕ .
При збільшенні кута ϕ зменшуються cosϕ й потужність P , а при зменшенні
кута ϕ активна потужність P зростає. Таким
чином, cosϕ показує, яка частина
повної потужності
теоретично може бути перетворена в інші види енергії.
Величина cosϕ називається коефіцієнтом потужності.
Для більш
раціонального використання потужності змінного струму,
вироблюваного джерелами
електричної енергії, потрібно намагатися зробити
навантаження таким, щоб cosϕ ланцюгу був
близький до одиниці. На практиці в масштабах підприємства добитися цього досить важко, і гарним
показником є cosϕ , рівний 0,9-0,95.