8. Числові методи розрахунку перехідних процесів електронних кіл

Розглянуті вище методи розрахунку перехідних процесів в електронних колах переважно придатні до розрахунку лінійних кіл. Це є  істотним недоліком, що обмежує сферу їхнього застосування. Як альтернативу розглянутим методам можна розглядати числові методи розрахунку перехідних процесів, які ґрунтуються на використанні числових методів інтегрування диференційних рівнянь, зокрема методів Ейлера, Рунге-Кутта тощо. Як відомо, числові методи розв’язання диференційних рівнянь з однаковим успіхом можуть бути застосовані до розв’язання як лінійних, так і нелінійних рівнянь, що істотно підвищує їхню практичну цінність. Також цими методами успішно розв’язують системи диференційних рівнянь доволі високих порядків, що робить їх придатними для розрахунку сучасних складних електронних пристроїв.

Нині числові методи розрахунку перехідних процесів електронних схем використовуються у двох варіантах:

1. Застосування традиційних числових методів розв’язання дифрівнянь.

2. Використання асоційованих дискретних моделей реактивних елементів електронних схем.

Перший спосіб полягає у формуванні математичної моделі електронного кола у вигляді рівняння чи системи дифрівнянь першого порядку, наприклад, як це робиться для класичного методу розрахунку перехідних процесів і подальшому числовому інтегруванню цих рівнянь. Допустимо, що математична модель електронного кола має такий вигляд:

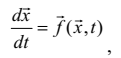                                                                 ,                                                            (4.41)

де 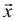  – вектор змінних, що описує електричний стан кола (деякі струми і напруги кола);

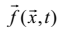   –     деяка вектор-функція, яка для лінійних кіл буде, очевидно, лінійною – і може бути подана так:

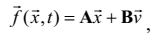                                          (4.42)

де A i B  деякі матриці коефіцієнтів, 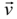  – вектор параметрів джерел енергії розглянутого кола.

            Застосувавши до розв’язання системи диференційних рівнянь неявний метод Ейлера, отримуємо таке різницеве рівняння:

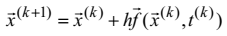                    (4.43)

де верхні індекси змінних визначають номер дискретного значення змінної,h   – крок інтегрування.

Другий підхід полягає у заміні реактивних елементів на кожному кроці інтегрування резистивними схемами заміщення. Розглянемо цей підхід  детальніше. Для цього запишемо рівняння котушки індуктивності

                                                                

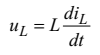
і перейдемо від неперервних змінних 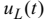 та 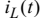 до їхніх дискрет   . 

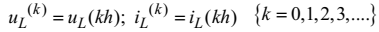Тоді згідно з неявним методом Ейлера наближено можна записати, що

 

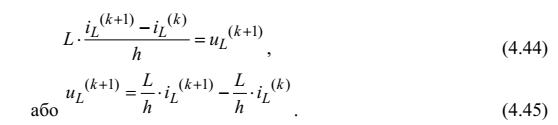
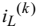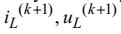Ураховуючи, що в ітераційному процесі величину  можна трактувати як відому, тобто постійну на цьому кроці інтегрування і змінними на (k+1) кроці інтегрування є величини , що дає змогу замінити на цьому кроці котушку індуктивності резистивною схемою заміщення (рис.4.20).

 

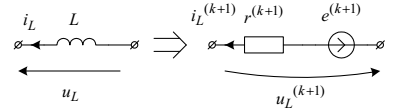
Рис. 4.20.  Схема заміщення котушки індуктивності на (к+1) кроці інтегрування,  асоційована до неявного методу Ейлера,

де .

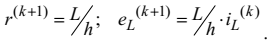
Аналогічна схема заміщення конденсатора показана на рис. 4.21, де

                                               .                                                   

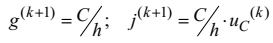
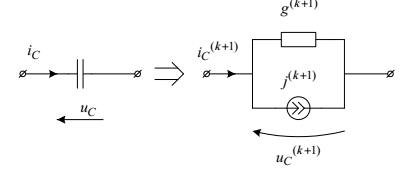Рис. 4.21.  Схема заміщення конденсатора на (к+1) кроці інтегрування, асоційована до неявного методу Ейлера

 

Замінивши у такий спосіб у реальній схемі всі реактивні елементи схемами заміщення, отримаємо резистивну схему з невідомими змінними.  Це є дискрети струмів та напруг на котушках індуктивності та конденсаторах, стосовно яких складаємо рівняння, розв’язання якого дає змогу одержати рекурентну формулу для визначення  дискретних значень (дискрет) струмів та напруг на реактивних елементах.

Для ілюстрації останнього підходу розглянемо приклад.

Приклад 4.9. Розрахуємо числовим методом перехідний процес у схемі, показаній на рис.4.22.


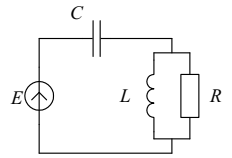
Рис. 4.22. Схема до прикладу 4.9

 

Після заміни реактивних елементів вказаної схеми резистивними схемами заміщення отримуємо резистивну схему (рис. 4.23).

 

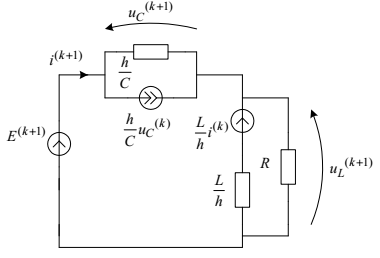
Рис.4.23.  Дискретна резистивна схема заміщення до прикладу 4.9

 Згідно із законами Ома та Кірхгофа запишемо систему рівнянь резистивного кола, показаного на рис. 4.22.

                                                                                                     

                                                                                                         

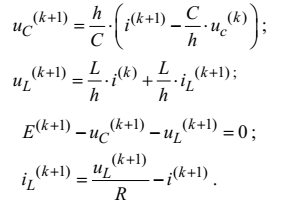
Розв’язавши цю систему рівнянь відносно змінної , одержуємо рекурентну формулу для визначення дискрет перехідного струму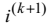 


                                              .
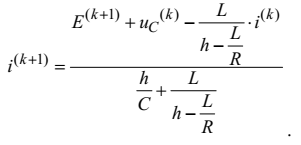