Тема 7. Основні характеристики та аналіз кіл змінного струму
| Сайт: | Освітній сайт КНУБА |
| Курс: | Основи теор. кіл, сигнали та проц. в електроніці (Ковал) |
| Книга: | Тема 7. Основні характеристики та аналіз кіл змінного струму |
| Надрукував: | Гість-користувач |
| Дата: | четвер, 29 січня 2026, 18:31 |
Опис
Тема 7. Основні характеристики та аналіз кіл змінного струму
1. Основні характеристики та аналіз кіл змінного струму
2. Аналіз усталених режимів кіл синусоїдного струму
3. Усталені режими електронних кіл, в яких діють несинусоїдні струми та напруги
4. Аналіз перехідних процесів електронних кіл
4.1. Класичний метод розрахунку
4.2. Операторний метод розрахунку перехідних процесів
4.3. Застосування інтеграла Дюамеля до розрахунку перехідних процесів
4.4. Числові методи розрахунку перехідних процесів електронних кіл
Зміст книги
- 1. Основні характеристики та аналіз кіл змінного струму
- 2. Аналіз усталених режимів кіл синусоїдного струму
- 3. Усталені режими електронних кіл, в яких діють несинусоїдні струми та напруги
- 4. Аналіз перехідних процесів електронних кіл
- 5. Класичний метод розрахунку перехідних процесів
- 6. Операторний метод розрахунку перехідних процесів
- 7. Застосування інтеграла Дюамеля до розрахунку перехідних процесів
- 8. Числові методи розрахунку перехідних процесів електронних кіл
1. Основні характеристики та аналіз кіл змінного струму
1. Основні характеристики та аналіз кіл змінного струму
Струм чи напруга, значення яких залежить від часу, називаються змінними. Відповідно електричні кола, у яких струми і напруги є змінними, називають електричними колами змінного струму.
Значення змінного струму (напруги ) у певний момент часу називають миттєвим значенням.
Якщо миттєві значення струму (напруги) задовольняють для усіх значень часу t таку умову
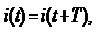 (4.13)
(4.13)
де – стала величина, яка називається періодом, то такі величини є періодичними.
Якщо ж закон зміни у часі струму (напруги) визначається таким виразом
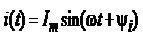 (4.14)
(4.14)
то такий струм (напруга) називається синусоїдним або гармонічним, а величина – амплітуда; – кутова частота; – початкова фаза – є його параметрами і пов’язані між собою такими самими співвідношеннями, як і для гармонічних сигналів.
Періодичні величини характеризуються певними інтегральними параметрами, зокрема для струму:
середнє значення 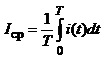 (4.15)
(4.15)
за період
діюче
значення 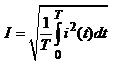 . (4.16)
. (4.16)
Подібно визначаються середнє та діюче значення напруги Uср, U
Для гармонічного струму 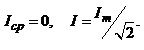
Важливими для кіл змінного струму є їхні енергетичні характеристики, основними з яких є такі
миттєва
потужність
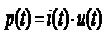 (4.17)
(4.17)
активна
потужність
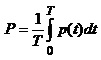 (4.18)
(4.18)
Енергетичний стан електричних кіл змінного синусоїдного струму характеризують потужності (активна, реактивна, повна), які зв’язані між собою так .
Як бачимо, активна потужність є середнім значенням миттєвої потужності за період і ця величина не залежить від часу. Одиниця вимірювання активної потужності – ват [Вт].
Для характеристики енергетичних властивостей кіл синусоїдного струму, як легко переконатись ,
де ( – початкова фаза напруги на елементі схеми).
Крім активної потужності, у колах синусоїдного струму використовують також поняття реактивної потужності (4.19) та повної потужності (4.20).
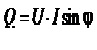 (4.19)
(4.19)
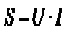 (4.20)
(4.20)
Одиниці вимірювання реактивної потужності – вольт-ампер реактивний [ВАР], а повної – вольт-ампер [ВА].
Фізичний зміст активної потужності – кількість електричної енергії за одиницю часу, яка перетворюється необоротно на інші види енергії (теплову, механічну тощо).
Реактивна потужність характеризує усереднене значення електричної енергії, якою обмінюються окремі елементи електричної схеми (реактивні елементи та джерела енергії).
2. Аналіз усталених режимів кіл синусоїдного струму
Електричними колами синусоїдного струму можуть бути лише лінійні кола, оскільки будь-який нелінійний елемент кола приводить до появи струмів чи напруг, що мають несинусоїдний характер.
Враховуючи те, що частота зміни струмів та напруг у лінійних схемах є величиною постійною і визначається параметрами джерел енергії, то в усталеному режимі кожен струм чи напруга характеризується двома параметрами – амплітудою та початковою фазою. Щоб відобразити ці параметри, для гармонічних струмів та напруг вводиться поняття комплексної амплітуди синусоїдної величини
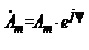 (4.21)
(4.21)
Символічний метод розрахунку дає змогу розрахувати усталені режими лінійних електричних кіл синусоїдного струму і як змінні використовує комплексні амплітуди струмів та напруг.
![]() – комплексна амплітуда синусоїдної
величини
– комплексна амплітуда синусоїдної
величини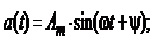 Am– амплітуда синусоїдної величини
Тобто є справедливим таке означення:
Am– амплітуда синусоїдної величини
Тобто є справедливим таке означення:
Комплексною амплітудою синусоїдної величини називають комплексне число, модуль якого дорівнює її амплітуді, а аргумент – початковій фазі.
Комплексна амплітуда однозначно описує синусоїдну величину за умови заданої частоти, тобто цю величину можна вважати комплексним зображенням змінної у часі синусоїдної величини. Замінивши у схемах реальні струми та напруги на їхні комплексні зображення (комплексні амплітуди), ми позбудемось часової залежності, що значно спрощує подальший аналіз кіл синусоїдного струму. Покажемо це на прикладах конкретних елементів електричних схем:
а) Резистор
Після підстановки у відоме співвідношення UR=RI виразу (4.14) для синусоїдного струму отримуємо
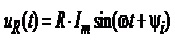 . Перейшовши у лівій і правій частинах цього виразу до комплексних амплітуд,
маємо
. Перейшовши у лівій і правій частинах цього виразу до комплексних амплітуд,
маємо
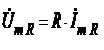 (4.22)
(4.22)
б) Котушка індуктивності
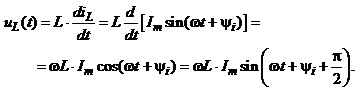
Знов-таки замінивши перший і останній вирази їхніми комплексними амплітудами, отримуємо:
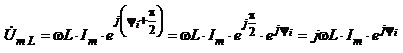 .
.
Або в остаточному вигляді
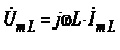 (4.23)
(4.23)
в) Конденсатор
Переходячи до комплексних зображень
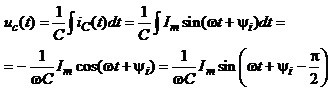 ,
,
одержуємо
. 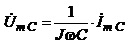 (4.24)
(4.24)
Вирази (4.22) – (4.24) показують, що для комплексних амплітуд струмів та напруг типових елементів існують алгебричні взаємозалежності, тобто так ми позбуваємось диференціальних чи інтегральних взаємозалежностей, які справедливі для миттєвих значень.
Узагальнюючи співідношення (4.22) – (4.24), їх можна подати у такому вигляді:
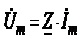 , (4.25)
, (4.25)
де Um та Im – комплексні амплітуди напруги та струму двополюсного елемента, – комплексний коефіцієнт, який називають комплексним опором цього двополюсника.
Вираз (4.25) називають законом Ома у комплексному вигляді.
Використовуючи прості тригонометричні перетворення, можна переконатись, що перехід від миттєвих значень струмів та напруг до їхніх комплексних амплітуд не порушує принципу суперпозиції і, отже, закони Кірхгофа, є справедливими і для комплексних амплітуд.
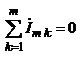 а)
а)
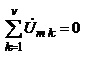 б)
. (4.26)
б)
. (4.26)
Наслідком співввідношень (4.25) та (4.26) є те, що для комплексних опорів, як і для опорів резисторів справедливі закони паралельного та послідовного з’єднання.
Комплексний опір деякого двополюсника Z як і будь-яке комплексне число, можна записати в алгебричному чи експоненціальному виглядах
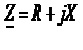 ,
,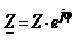
де R – активний опір двополюсника;
X – реактивний опір двополюсника;
Z – повний опір (модуль комплексного опору);
ф – аргумент комплексного опору.
Очевидно, справедливими є такі співвідношення
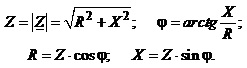
Модуль комплексного опору котушки
індуктивності 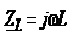 називають індуктивним опором і
позначають через XL, а модуль комплексного опору конденсатора
називають
називають індуктивним опором і
позначають через XL, а модуль комплексного опору конденсатора
називають 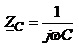 ємнісним опором та
позначають через XC
ємнісним опором та
позначають через XC
Фізичний зміст комплексного опору такий:
модуль комплексного опору (повний опір) показує, у скільки разів амплітуда напруги на елементі перевищує амплітуду струму, а аргумент є різницею початкових фаз (зсувом фаз) напруги та струму.
Поряд із поняттям комплексного опору використовується поняття комплексної провідності, яка є оберненою до опору
![]() .
.
Введені у такий спосіб комплексні амплітуди струмів та напруг і комплексні опори дають змогу розраховувати електричні кола змінного синусоїдного струму, тобто кола, які складаються з резисторів, котушок індуктивності, конденсаторів, джерел гармонічної напруги чи струму, подібно, як це було у резистивних схемах.
Відповідний метод аналізу часто називають символічним методом або методом комплексних амплітуд.
Суть названого методу така.
Крок 1. Як змінні, що характеризують електричний стан схеми, вибираємо комплексні амплітуди струмів та напруг.
Крок 2. Реальні елементи електричної схеми замінюють їхніми комплексними опорами.
Крок 3. Використовуючи той чи інший метод з п. 2.3, будують математичну модель схеми у вигляді системи комплексних рівнянь.
Крок 4. Розв’язавши отримані на кроці 3 рівняння, знаходять комплексні амплітуди шуканих струмів та напруг.
Крок 5. За знайденими на попередньому кроці комплексними амплітудами відтворюють відповідні миттєві значення струмів та напруг.
3. Усталені режими електронних кіл, в яких діють несинусоїдні струми та напруги
Будь-яку періодичну несинусоїдну величину можна записати у вигляді ряду Фур’є, тобто суми гармонічних складових з різними частотами
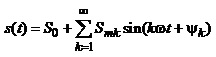 . (4.27)
. (4.27)
Також відомо, що у лінійних системах, зокрема електричних колах, справедливим є принцип суперпозиції. Стосовно до електричних кіл його можна сформулювати так.
Розрахунок лінійних електричних кіл змінного несинусоїдного струму здійснюється символічним методом для кожної гармоніки зокрема.
Струм (напруга), зумовлений дією декількох джерел енергії, дорівнює сумі струмів, породжених кожним джерелом зокрема. Якщо в електричному колі є джерело періодичного несинусоїдного струму чи напруги, то таке джерело можемо замінити низкою паралельно або послідовно з’єднаних джерел енергії, кожне з яких є гармонічним з частотою . Тоді, розраховуючи схему з одним джерелом, що відображає одну гармоніку, отримуємо частковий розв’язок для шуканої змінної, а підсумовуючи ці часткові розв’язки, одержаний ряд типу Фур’є, який відображає цю змінну. Очевидно, для розрахунку кожної гармоніки шуканої величини необхідно використовувати символічний метод аналізу, пам’ятаючи про залежність комплексного опору елементів схеми від частоти. Звичайно при такому підході застосовують усічений ряд Фур’є, тобто враховують скінченну кількість гармонік у спектрі, що зумовлює певну похибку обчислень.
4. Аналіз перехідних процесів електронних кіл
Перехідними процесами в електричних колах називаються процеси, які виникають під час переходу від одного усталеного стану до іншого.
Перехідні процеси в електричних колах часто зумовлюють значні хоча і короткочасні зміни струмів та напруг кола, що може призвести до виходу з ладу електронних пристроїв.
Такий перехід зумовлюється комутаціями, тобто під’єднанням чи від’єднанням від електричного кола того чи іншого елемента. Перехідні процеси виникають в колах як постійного, так і змінного струмів, однак необхідною умовою є наявність у колі реактивних елементів, бо саме реактивні елементи можуть нагромаджувати електричну енергію і тим самим зумовлюють інерційність процесів у колі.
Потреба у розрахунку перехідних процесів зумовлена, переважно двома причинами:
По-перше, під час комутацій в електричних колах можуть виникати різкі збільшення напруг та струмів, що призводить до виходу з ладу компонент електричних кіл, особливо електронних елементів.
По-друге, часто важливим є час переходу електричної схеми із одного усталеного стану (стаціонарного режиму) в інший, що визначає швидкодію відповідного пристрою, а його можна оцінити, лише розрахувавши перехідний процес.
Для розрахунку перехідних процесів в електричних колах існує декілька методів: операторний, інтеграл Дюамеля, класичний, числовий. Перші два методи придатні до розрахунку лише лінійних кіл, а два останні методи є універсальними і стосуються як лінійних, так і нелінійних кіл.
5. Класичний метод розрахунку перехідних процесів
Суть цього методу полягає у формуванні математичної моделі схеми у вигляді диференційного рівняння чи системи диференційних рівнянь, які розв’язуються традиційними методами теорії дифрівнянь. Змінними у такій математичній моделі є миттєві значення струмів та напруг. Причому найзручніше вибрати змінними струми у котушках індуктивності та напруги на конденсаторах, які визначають енергетичний стан кола. Крім цього, напруги на конденсаторах і струми у котушках індуктивності визначають значення змінних у початковий момент часу (початкові умови), які є необхідними для запису роз’язку диференційного рівняння.
Проілюструємо класичний метод розрахунку перехідних процесів на простому прикладі.
Наведемо два закони комутації, які дозволяють визначити початкові
умови, необхідні для отримання розв’язку диференційного рівняння.
1–й закон Струм у котушці індуктивності не може змінюватися стрибкоподібно.
2–й закон Напруга на конденсаторі не може змінюватися стрибкоподібно.
6. Операторний метод розрахунку перехідних процесів
Цей метод розрахунку ґрунтується на відомому перетворенні Лапласа функцій часу.
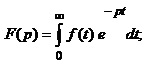 а)
а)
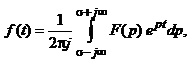 б) (4.28)
б) (4.28)
де f(t) – деяка функція часу (оригінал), причому f(t)=0 для t<0 .
F(p) – зображення за Лапласом функції f(t);
p – комплексна змінна.
Перетворення (4.28а) називають прямим, а (4.28б) – зворотним.
Суть операторного методу полягає у тому, що для описання електричного кола замість миттєвих значень струмів та напруг використовують їхні операторні зображення I(p), U(p).
Внаслідок лінійності перетворення Лапласа закони Кірхгофа справедливі і для операторних зображень струмів та напруг i(t), u(t), а зв’язок між операторними зображеннями струмів та напруг на основних елементах схеми можна отримати так.
Резистор
ℒ
, 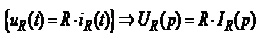 (4.29)
(4.29)
Котушка індуктивності
ℒ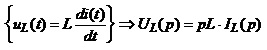 , (4.30)
, (4.30)
Конденсатор
ℒ
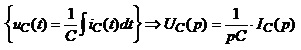 . (4.31)
. (4.31)
Зауважимо, що співвідношення (4.30) та (4.31) отримані за умови нульових значень початкового струму в котушці та початкової напруги на конденсаторі.
Узагальнюючи формули (4.29) – (4.31), як і за символічним методом, можна одержати такий вираз
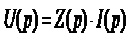 , (4.32)
, (4.32)
який називають законом Ома в операторній формі, а коефіцієнт – операторним опором двополюсника. Відповідно для окремих елементів схеми:
R – операторний опір резистора,
pL – операторний опір котушки індуктивності,
1/pC – операторний опір конденсатора.
Також існує поняття комплексної провідності, яка є оберненою величиною до .
Для операторних опорів та провідностей теж справедливі закони паралельного та послідовного з’єднання.
Алгоритм розрахунку перехідних процесів операторним методом подібний до алгоритму символічного методу і його можна подати у вигляді такої послідовності кроків.
Крок 1. Замінюємо всі струми та напруги електричної схеми їхніми операторними зображеннями, а елементи схеми описуємо операторними опорами чи провідностями.
Крок 2. Записуємо математичну модель схеми щодо тих чи інших операторних струмів та напруг, використовуючи традиційні методи, описані у розділі 2.
Крок 3. За допомогою розрахунку знаходимо зазначені операторні зображення струмів чи напруг.
Крок 4. За відомими операторними зображеннями струмів та напруг відтворюємо їхні оригінали, тобто записуємо миттєві значення струмів та напруг.
Щодо виконання кроку 4, як правило, його реалізовують не з допомогою інтеграла (4.28б), а на підставі теореми про лишки, частинним видом якої є теорема Хевісайда.
Вказана теорема ґрунтується на тому, що операторні зображення струмів чи напруг електричного кола є, як правило, відношенням степеневих поліномів змінної .
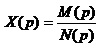 , (4.33)
, (4.33)
де 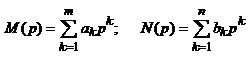 .
.
Тоді полюси функції X(p) отримують як розв’язки такого рівняння N(p):
.
Позначивши ці полюси через і допускаючи, що вони всі різні, одержуємо запис теореми Хевісайда у такому вигляді:
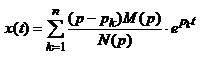 , (4.34)
, (4.34)
де –миттєве значення струму чи напруги.
Для зручності наведемо таблицю найвживаніших в теорії кіл оригіналів та їхніх зображень:

Рис. 4.15. Операторні зображення деяких часових функцій
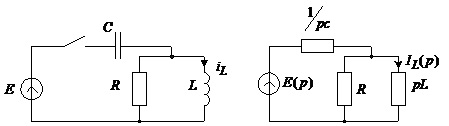
Приклад 4.7. Знайдемо перехідний струм схеми, зображеної на рис.4.16, а
|
а |
б |
Рис.4.16. Схема до прикладу 4.7
Виконавши крок 1 алгоритму, отримуємо схему, показану на рис.4.16, б. Операторне зображення ЕРС джерела, яке під’єднується в нульовий момент часу до схеми, дорівнює , оскільки у часовій області вмикання відображається функцією Хевісайда. Знайдемо вираз для операторного зображення струму у котушці.
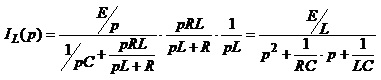 .
.
Використавши (4.34), визначимо миттєве значення струму . Для цього знайдемо полюси
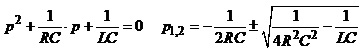
Врахувавши, що
знаменник виразу для
якщо відомі полюси, можна подати так
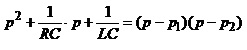 ,
,
знайдемо перехідний струм у котущці:
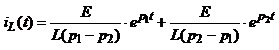 .
.
Проаналізуємо останній вираз, врахувавши, що полюси залежно від значення параметрів схеми можуть набувати як дійсні значення, так і комплексні. Причому умовою того, щоб полюси були дійсними, є така нерівність
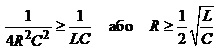 ,
,
набувають від’ємні значення і тому графік перехідного процесу виглядатиме так, як це показано на рис.4.17, а.
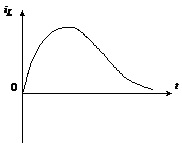
Рис.4.17а. Вигляд перехідного процесу при дійсних значеннях полюсів
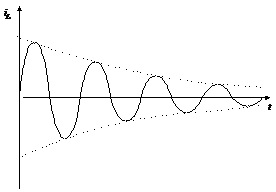
Рис.4.17б. Вигляд перехідного процесу у разі комплексноспряжених полюсів
Зауважимо, що такий вид перехідного процесу називається аперіодичним.
Якщо ж полюси набувають комплексноспряжені значення, тобто , характер перехідного процесу якісно змінюється. Покажемо це аналітично
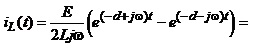
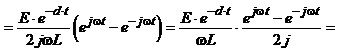
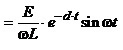
Як видно з останнього виразу, у такому разі перехідний струм є синусоїдою, амплітуда якої з часом зменшується. (рис.4.17, б). Такий вид перехідного процесу називають коливним.
7. Застосування інтеграла Дюамеля до розрахунку перехідних процесів
Цей метод застосовується, коли потрібно визначити перехідну напругу чи струм у деякому елементі схеми, зумовлені під’єднанням до схеми джерела, струм чи напруга якого мають складну форму.
Для розрахунку перехідного процесу задану схему подамо у вигляді, наведеному на рис.4.18.
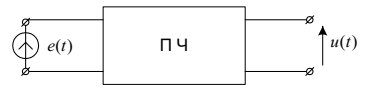
Рис.4.18. Подання схеми під час перехідного процесу за допомогою інтеграла Дюамеля
На рис.4.18 – джерело змінної ЕРС, вмикання якого зумовлює перехідний процес, – вихідна напруга, яку потрібно визначити.
Введемо поняття операторного коефіцієнта передавання напруги для прохідного чотириполюсника ПЧ
, 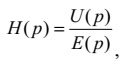 (4.35)
(4.35)
де – операторне зображення вихідної напруги чотириполюсника;
– операторне зображення вхідної напруги.
Якщо припустити, що вхідним сигналом є напруга у вигляді (функція Дірака), операторне зображення якої згідно з табл. 4.15 дорівнює одиниці, то з (4.35) випливає
. 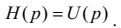 (4.36)
(4.36)
А це означає, що операторний коефіціент є не що інше, як зображення за Лапласом вихідної напруги чотириполюсника при поданні на його вхід сигналу у вигляді - імпульсу.
Цю напругу позначають
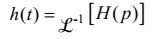 (4.37)
(4.37)
і називають імпульсною характеристикою чотириполюсника ПЧ.
Перепишемо співвідношення (4.35) у дещо іншому вигляді
і застосуємо до лівої і правої частин зворотне перетворення Лапласа, використавши інтеграл згортки.
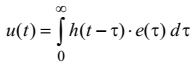 (4.38)
(4.38)
Отриманий у такий спосіб вираз називають інтегралом Дюамеля і він дає змогу визначити перехідну напругу у схемі у разі вмикання змінної напруги будь-якої форми.
Інтеграл Дюамеля можна обчислити як аналітично, так і числовими методами.
Зауважимо, що вираз (4.38) придатний для розрахунку перехідної напруги лише за умови нульових початкових умов, тобто коли . Якщо ж така умова не виконується, то для розрахунку перехідних процесів варто користуватися таким виразом
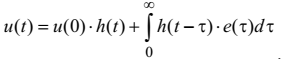 (4.39)
(4.39)
Доволі часто для характеристики перехідних процесів у колі використовують перехідну характеристику , тобто значення вихідної напруги чотириполюсника ПЧ при вхідному сигналі у формі функції Хевісайда . Зв’язок між імпульсною перехідною характеристикою кола та її перехідною характеристикою такий:
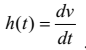 (4.40)
(4.40)
Зручність використання перехідної характеристики електронного кола для обчислення інтеграла Дюамеля полягає у можливості її експериментального визначення.
Приклад 4.8. Розрахуємо перехідний процес у послідовному з’єднанні резистора та конденсатора (рис. 4.19, а), під’єднаних до джерела змінної напруги (рис. 4.19, б).
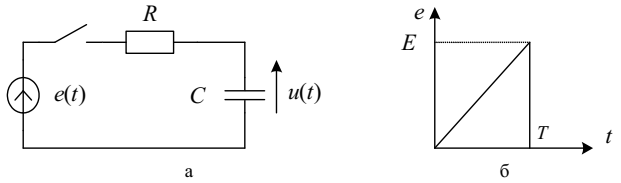
|
а |
б |
Рис. 4.19. Схема до прикладу 4.8
Знайдемо передавальну функцію згідно з виразом (4.35)
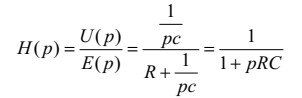 .
.
Враховуючи, що є операторним зображенням імпульсної перехідної характеристики цього кола, визначимо її.
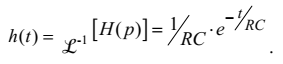
Перехідну напругу на конденсаторі доцільно визначати для двох випадків
–
–
коли 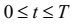 (тобто під час дії вхідного
сигналу),
(тобто під час дії вхідного
сигналу),
–
–
коли 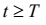 (після закінчення дії вхідного
сигналу).
(після закінчення дії вхідного
сигналу).
Допустивши, що початкова напруга конденсатора нульова, для першого випадку згідно з (4.38) одержимо
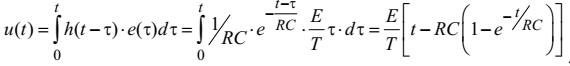 .
.
У другому випадку, врахувавши що при дорівнює 0, перехідна напруга на конденсаторі розраховується так:
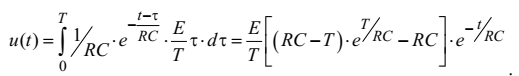
.
8. Числові методи розрахунку перехідних процесів електронних кіл
Розглянуті вище методи розрахунку перехідних процесів в електронних колах переважно придатні до розрахунку лінійних кіл. Це є істотним недоліком, що обмежує сферу їхнього застосування. Як альтернативу розглянутим методам можна розглядати числові методи розрахунку перехідних процесів, які ґрунтуються на використанні числових методів інтегрування диференційних рівнянь, зокрема методів Ейлера, Рунге-Кутта тощо. Як відомо, числові методи розв’язання диференційних рівнянь з однаковим успіхом можуть бути застосовані до розв’язання як лінійних, так і нелінійних рівнянь, що істотно підвищує їхню практичну цінність. Також цими методами успішно розв’язують системи диференційних рівнянь доволі високих порядків, що робить їх придатними для розрахунку сучасних складних електронних пристроїв.
Нині числові методи розрахунку перехідних процесів електронних схем використовуються у двох варіантах:
1. Застосування традиційних числових методів розв’язання дифрівнянь.
2. Використання асоційованих дискретних моделей реактивних елементів електронних схем.
Перший спосіб полягає у формуванні математичної моделі електронного кола у вигляді рівняння чи системи дифрівнянь першого порядку, наприклад, як це робиться для класичного методу розрахунку перехідних процесів і подальшому числовому інтегруванню цих рівнянь. Допустимо, що математична модель електронного кола має такий вигляд:
, 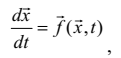 (4.41)
(4.41)
де 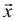 – вектор змінних, що описує електричний стан кола (деякі струми і напруги
кола);
– вектор змінних, що описує електричний стан кола (деякі струми і напруги
кола);
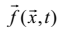 – деяка вектор-функція, яка для лінійних кіл буде, очевидно, лінійною – і
може бути подана так:
– деяка вектор-функція, яка для лінійних кіл буде, очевидно, лінійною – і
може бути подана так:
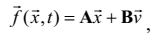 (4.42)
(4.42)
де A i B деякі матриці коефіцієнтів, 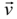 – вектор параметрів джерел енергії розглянутого кола.
– вектор параметрів джерел енергії розглянутого кола.
Застосувавши до розв’язання системи диференційних рівнянь неявний метод Ейлера, отримуємо таке різницеве рівняння:
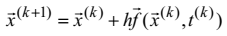 (4.43)
(4.43)
де верхні індекси змінних визначають номер дискретного значення змінної,h – крок інтегрування.
Другий підхід полягає у заміні реактивних елементів на кожному кроці інтегрування резистивними схемами заміщення. Розглянемо цей підхід детальніше. Для цього запишемо рівняння котушки індуктивності
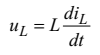
і перейдемо від неперервних змінних 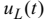 та
та 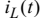 до їхніх дискрет
.
до їхніх дискрет
.
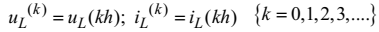 Тоді згідно з неявним методом Ейлера наближено можна записати, що
Тоді згідно з неявним методом Ейлера наближено можна записати, що
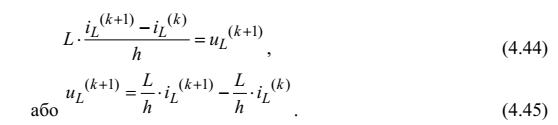
Ураховуючи, що в ітераційному
процесі величину 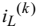 можна трактувати як відому, тобто постійну на
цьому кроці інтегрування і змінними на (k+1) кроці інтегрування є
величини
можна трактувати як відому, тобто постійну на
цьому кроці інтегрування і змінними на (k+1) кроці інтегрування є
величини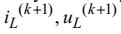 , що дає змогу замінити на цьому
кроці котушку індуктивності резистивною схемою заміщення (рис.4.20).
, що дає змогу замінити на цьому
кроці котушку індуктивності резистивною схемою заміщення (рис.4.20).
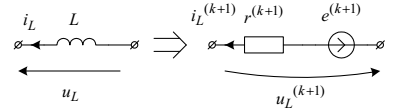
Рис. 4.20. Схема заміщення котушки індуктивності на (к+1) кроці інтегрування, асоційована до неявного методу Ейлера,
де
.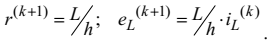
Аналогічна схема заміщення конденсатора показана на рис. 4.21, де
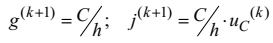
 .
.
Рис. 4.21. Схема заміщення конденсатора на (к+1) кроці інтегрування, асоційована до неявного методу Ейлера
Замінивши у такий спосіб у реальній схемі всі реактивні елементи схемами заміщення, отримаємо резистивну схему з невідомими змінними. Це є дискрети струмів та напруг на котушках індуктивності та конденсаторах, стосовно яких складаємо рівняння, розв’язання якого дає змогу одержати рекурентну формулу для визначення дискретних значень (дискрет) струмів та напруг на реактивних елементах.
Для ілюстрації останнього підходу розглянемо приклад.
Приклад 4.9. Розрахуємо числовим методом перехідний процес у схемі, показаній на рис.4.22.
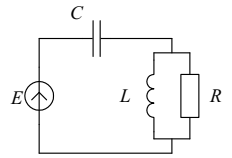
Рис. 4.22. Схема до прикладу 4.9
Після заміни реактивних елементів вказаної схеми резистивними схемами заміщення отримуємо резистивну схему (рис. 4.23).
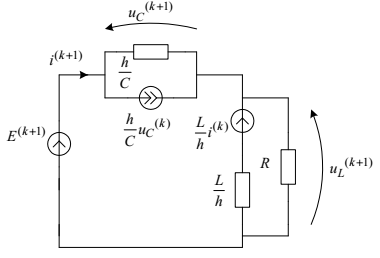
Рис.4.23. Дискретна резистивна схема заміщення до прикладу 4.9
Згідно із законами Ома та Кірхгофа запишемо систему рівнянь резистивного кола, показаного на рис. 4.22.
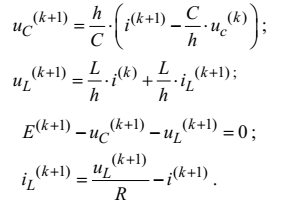
Розв’язавши цю систему рівнянь
відносно змінної
, одержуємо рекурентну формулу для визначення дискрет перехідного струму 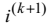
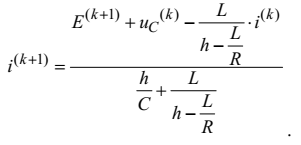
.