Тема 7. Основні характеристики та аналіз кіл змінного струму

            Цей метод розрахунку ґрунтується на відомому перетворенні Лапласа функцій часу.

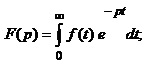  а) 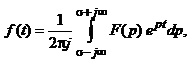      б)     (4.28)

де  f(t)  – деяка функція часу (оригінал), причому f(t)=0 для t<0  .

   F(p)  – зображення за Лапласом функції f(t);

        p   – комплексна змінна.

            Перетворення (4.28а) називають прямим, а (4.28б) – зворотним.

         Суть операторного методу полягає у тому, що для описання електричного кола замість миттєвих значень струмів та напруг  використовують їхні операторні зображення I(p), U(p).

         Внаслідок лінійності перетворення Лапласа закони Кірхгофа справедливі і для операторних зображень струмів та напруг i(t), u(t), а зв’язок між операторними зображеннями струмів та напруг на основних елементах схеми можна отримати так.

Резистор

     ℒ , 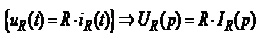    (4.29)

Котушка індуктивності 

  ℒ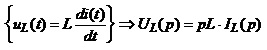 ,   (4.30)

Конденсатор

  ℒ 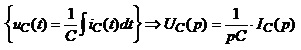.     (4.31)

            Зауважимо, що співвідношення (4.30) та (4.31) отримані за умови нульових значень початкового струму в котушці та початкової напруги на конденсаторі.

            Узагальнюючи формули (4.29) – (4.31), як і за символічним методом, можна одержати такий вираз

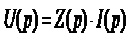                   ,           (4.32)

який називають законом Ома в операторній формі, а коефіцієнт – операторним опором двополюсника. Відповідно для окремих елементів схеми:

        R      – операторний опір резистора,

    pL  – операторний опір котушки індуктивності,

1/pC – операторний опір конденсатора.

            Також існує поняття комплексної провідності, яка є оберненою величиною до .

            Для операторних опорів та провідностей теж справедливі закони паралельного та послідовного з’єднання.

            Алгоритм розрахунку перехідних процесів операторним методом подібний до алгоритму символічного методу і його можна подати у вигляді такої послідовності кроків.

            Крок 1. Замінюємо всі струми та напруги електричної схеми їхніми операторними зображеннями, а елементи схеми описуємо операторними опорами чи провідностями.

            Крок 2. Записуємо математичну модель схеми щодо тих чи інших операторних струмів та напруг, використовуючи традиційні методи, описані у розділі 2.

            Крок 3. За допомогою розрахунку знаходимо зазначені опера­торні зображення струмів чи напруг.

            Крок 4. За відомими операторними зображеннями струмів та напруг відтворюємо їхні оригінали, тобто записуємо миттєві значення струмів та напруг.

            Щодо виконання кроку 4, як правило, його реалізовують не з допомогою інтеграла (4.28б), а на підставі теореми про лишки, частинним видом якої є теорема Хевісайда.

            Вказана теорема ґрунтується на тому, що операторні зображення струмів чи напруг електричного кола є, як правило, відношенням степеневих поліномів змінної .

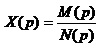     ,        (4.33)

де .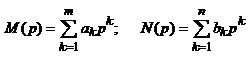

Тоді полюси функції X(p) отримують як розв’язки такого рівняння N(p):

                                                                   .                                                                       

Позначивши ці полюси через  і допускаючи, що вони всі різні, одержуємо запис теореми Хевісайда у такому вигляді:

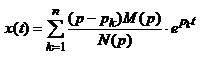      ,          (4.34)

де –миттєве значення струму чи напруги.

            Для зручності наведемо таблицю найвживаніших в теорії кіл оригіналів та їхніх зображень:

 

Рис. 4.15.  Операторні зображення деяких часових функцій

 

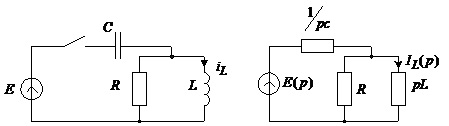
Приклад 4.7.  Знайдемо перехідний струм  схеми, зображеної на рис.4.16, а

Рис.4.16.  Схема до прикладу 4.7

 

Виконавши крок 1 алгоритму, отримуємо схему, показану на рис.4.16, б. Операторне зображення ЕРС джерела, яке під’єднується в нульовий момент часу до схеми, дорівнює , оскільки у часовій області вмикання відображається функцією Хевісайда. Знайдемо вираз для операторного зображення струму у котушці.

                            .                                

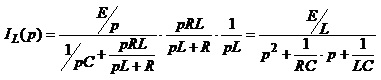Використавши  (4.34), визначимо миттєве значення струму . Для цього знайдемо полюси

                       

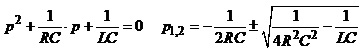
Врахувавши, що знаменник виразу для  якщо відомі полюси, можна подати так

                                             ,                                                 

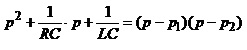знайдемо перехідний струм у котущці:

                                         .                                             

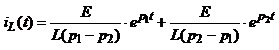Проаналізуємо останній вираз, врахувавши, що полюси  залежно від значення параметрів схеми можуть набувати як дійсні значення, так і комплексні. Причому умовою того, щоб полюси були дійсними, є така нерівність

           ,                                                    

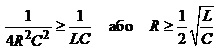 набувають від’ємні значення і тому графік перехідного процесу виглядатиме так, як це показано на рис.4.17, а.

 

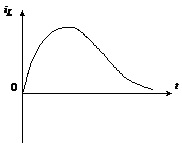
Рис.4.17а.  Вигляд перехідного процесу при дійсних значеннях полюсів

 

 

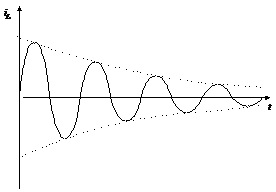
Рис.4.17б.  Вигляд перехідного процесу у разі комплексноспряжених полюсів

 

            Зауважимо, що такий вид перехідного процесу називається аперіодичним.

            Якщо ж полюси набувають комплексноспряжені значення, тобто  , характер перехідного процесу якісно змінюється. Покажемо це аналітично

                                              

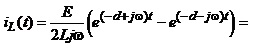
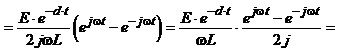
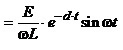
     Як видно з останнього виразу, у такому разі перехідний струм є синусоїдою, амплітуда якої з часом зменшується. (рис.4.17, б). Такий вид перехідного процесу називають коливним.