Тема 5. Моделі компонентів електронних кіл
Моделі компонентів електронних кіл.
1. Загальні питання
2. Схема заміщення напівпровідникового діода
3. Моделі біполярного транзистора
4. Моделі польових транзисторів
5. Моделі електронної лампи (тріода)
3. Моделі біполярного транзистора
Найдетальніше відображає процеси у біполярному транзисторі п-р-п-типу еквівалентна схема Еберса –Молла, показана на рис.3.31.
Для транзистора типу p-n-p необхідно у цій моделі змінити полярності вмикання діодів на протилежні, а також вибрані додатні напрями струмів та напруг.
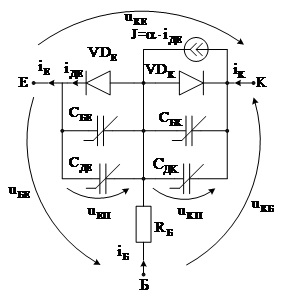
Рис. 3.31. Еквівалентна схема Еберса–Молла біполярного транзистора типу n-p-n
У моделі, показаній на рис. 3.31, діоди VDE та VDK відображають відповідно емітерний та колекторний переходи. Кероване джерело струму J = a×іДЕ моделює передавання струму з емітера в колектор. Ємності СБЕ та СБК – це нелінійні бар’єрні ємності емітерного та колекторного переходів, а СДЕ та СДК – їхні дифузійні ємності. Резистор RБ відображає опір базової області транзистора. У відповідній довідковій літературі наведено формули для розрахунку параметрів компонент цієї моделі. Найчастіше враховують залежності бар’єрних ємностей від напруг uЕП та uКП на переходах та залежність коефіцієнта a від напруг та струмів.
В аналізі електронних схем у режимі слабких сигналів (лінійні підсилювачі, лінійні фільтри тощо) використовують лінеаризовані малосигнальні еквівалентні схеми біполярних транзисторів, які пов’язують між собою малі відхилення струмів та напруг стосовно значень у статичній робочій точці.
Це означає, що в еквівалентній схемі транзистора (рис. 3.31) нелінійні елементи замінюють лінійними, значення параметрів яких дорівнюють значенням диференційних параметрів, визначених в статичній робочій точці. Так, діоди VDE та VDK замінюють диференційними опорами RБЕ та RКБ, бар’єрні ємності СБЕ та СБК – диференційними ємностями, які в сумі з відповідними дифузійними ємностями утворюють ємності емітерного переходу СЕП та колекторного переходу СКП. Отже, еквівалентна малосигнальна схема біполярного транзистора набуває вигляду, зображеного на рис. 3.32. Наявність ємностей СЕП та СКП у цій еквівалентній схемі дає змогу відобразити частотні властивості транзистора, які проявляються в діапазоні високих частот (сотні кГц і вище). Орієнтовні значення параметрів елементів еквівалентної схеми: RБ та RБЕ – десятки Ом – одиниці кОм; RКБ – десятки – сотні кОм; a = 0,95 – 0,995; СЕП – сотні – тисячі пФ; СКП – одиниці – сотні пФ.
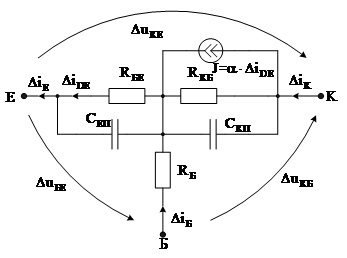
Рис. 3.32. Еквівалентна малосигнальна схема біполярного транзистора
У діапазоні низьких частот впливом ємностей можна знехтувати, і в такому разі малосигнальні параметри можна безпосередньо визначати на підставі ВАХ транзистора.
Спосіб визначення параметрів diБ/duБЕ та diБ/duКЕ у деякій робочій точці А на підставі вхідних ВАХ для схеми вмикання транзистора із спільним емітером подано на рис. 3.33.
|
а |
б |
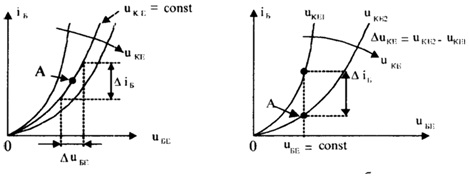
Рис. 3.33. Визначення низькочастотних малосигнальних параметрів транзистора на підставі вхідних ВАХ
Отже, як бачимо з рис. 3.33, а, параметр diБ/duБЕ » DiБ/DuБЕ, якщо uКЕ = =const. Його фізичний зміст – вхідна провідність транзистора для малих приростів струму iБ та напруги uБЕ у разі вмикання транзистора зі спільним емітером. Позначимо його gББ.
З рис. 3.33,
б випливає, що diБ /duКЕ » DiБ /DuКЕ, якщо uБЕ =
= const. Фізичний зміст цього параметра – зворотна прохідна провідність
транзистора для малих приростів струму iБ та напруги uКЕ.
Позначимо цей параметр gБК. Оскільки при DuКЕ > 0 приріст струму DiБ <0, то
gБК < 0.
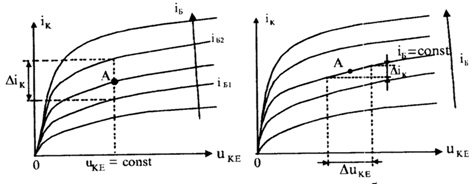
Спосіб визначення параметрів diK/diБ та diK/duKE в деякій робочій точці А на підставі вихідних ВАХ транзистора, увімкненого за схемою із спільним емітером, подано на рис. 3.34.
а | б |
Рис. 3.34. Визначення
низькочастотних малосигнальних
параметрів транзистора на підставі
вихідних ВАХ
Із рис. 3.34, а бачимо, що параметр diK / diБ » DiK /DiБ, якщо uКЕ = const. Його фізичний зміст – коефіцієнт передавання струму з бази в колектор, який було позначено як bдиф.
Із рис. 3.34, б бачимо, що параметр diK/duKE » DiK/DuKE, якщо iБ = const. Фізичний зміст цього параметра – вихідна провідність транзистора для малих приростів струму iK та напруги uKE. Позначимо цей параметр gKK.
Отже, з урахуванням прийнятих позначень, можемо записати співвідношення (3.41):
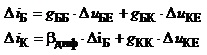 , (3.41)
, (3.41)
які в сукупності утворюють математичну модель біполярного транзистора у режимі малих сигналів.
У другому розділі зазначено, що лінеаризовані багатополюсники доцільно описувати компонентними рівняннями типу (2.24), в яких усі лінеаризовані параметри є провідностями. Для транзистора ці рівняння мають вигляд:
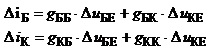 . (3.42)
. (3.42)
Порівнюючи рівняння (3.41) та (3.42), бачимо, що вони відрізняються лише першими доданками останніх рівнянь. Одночасно легко переконатись, що параметр gКБ, який дорівнює відношенню DiK /DuБE, якщо uКE = const, можна визначити через параметри рівняння (3.41):
![]() .
.
Отже, компонентні рівняння біполярного транзистора як лінеаризованого багатополюсника можна записати так:
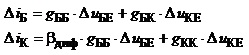 . (3.43)
. (3.43)
У матрицевій формі ці рівняння набувають вигляду:
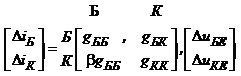 , (3.44)
, (3.44)
що відповідає рівнянню в у–параметрах триполюсника, яким є транзистор. Схемне зображення такого триполюсника подано на рис. 3.35.
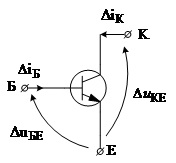
Рис.3.35. Біполярний транзистор як триполюсник