5. Метод контурних струмів

 Ця математична модель використовує як змінні, що характеризують електричний стан кола, контурні струми, тобто струми, які циркулюють у деякому контурі схеми. Контурні струми і струми елементів електричної схеми пов’язані простими лінійними співвідношеннями, а саме струм будь-якого елемента схеми визначається як алгебрична сума контурних струмів контурів, у які цей елемент входить. Знак доданка у цій сумі визначається співвідношенням напрямків струмів контурів і струму цього елемента.

Зауважимо, що у цьому методі беруться до уваги контурні струми лише системи незалежних контурів.

Для виведення рівнянь контурних струмів розглянемо електричну схему, що складається з резисторів та джерел ЕРС, тобто в загальному випадку кожен елемент можна подати як неідеальне джерело ЕРС (рис.2.11, а). На підставі другого закону Кірхгофа запишемо рівняння для деякого контуру


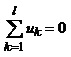
і врахувавши співвідношення (2.9а), отримаємо

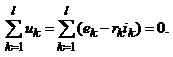                                                   (2.18)

Визначимо струми окремих елементів схеми через контурні струми

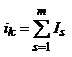                ,                                                              (2.19)

де Is – контурні струми контурів до складу яких входить k-й елемент схеми. Виконавши певні перестановки у рівнянні (2.18) і врахувавши співвідношення (2.19), одержимо рівняння контурних струмів для вибраного контуру у такому вигляді

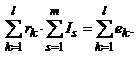                                                                      (2.20)

Записавши такі рівняння для всіх контурів із незалежної системи контурів, отримаємо систему рівнянь контурних струмів для розглянутої схеми, яку зручно записати у матричному вигляді

                            ,                                                                (2.21)

де Z – матриця опорів системи рівнянь контурних струмів; E– вектор ЕРС контурів; I – вектор контурних струмів. Елементи матриці Z та вектор E визначаються за такими правилами.

            Діагональні елементи матриці Z є сумою опорів компонентів схеми, що утворюють контур, який відповідає цьому елементу.

            Позадіагональний елемент матриці Z є сумою опорів компонентів схеми, які є спільними для двох контурів, що відповідають цьому елементу, причому ця сума береться із знаком “+”, якщо напрямки обходів контурів у спільних елементах схеми збігаються і “–” коли вони є протилежними.

            Компоненти вектора E дорівнюють алгебричній сумі ЕРС джерел, які входять у відповідний  контур.

            Приклад 2.3 Складемо рівняння контурних струмів для такої схеми.


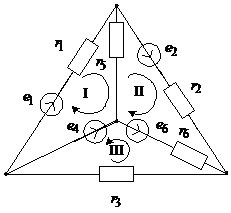
Рис.2.15. Схема до прикладу 2.3

            Систему незалежних контурів цієї схеми утворюють три контури, позначені римськими цифрами. Додатні напрямки обходу контурів показані на рис.2.15. Запишемо матрицю Z та вектор E для цієї схеми згідно з наведеними вище правилами.

  


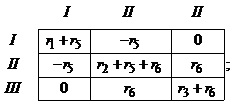
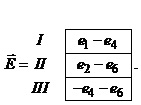
Навпроти рядків та стовпчиків матриці Z та вектора  вказані відповідні контури.