Тема 3. Математичні моделі електричних схем
| Сайт: | Освітній сайт КНУБА |
| Курс: | Основи теор. кіл, сигнали та проц. в електроніці (Ковал) |
| Книга: | Тема 3. Математичні моделі електричних схем |
| Надрукував: | Гість-користувач |
| Дата: | субота, 21 лютого 2026, 21:40 |
Опис
Математичні моделі електричних схем
1. Математичні моделі електричних схем з двополюсниками1.1. Повна система рівнянь електричної схеми
1.3. Метод вузлових напруг
1.2. Формулювання законів Кірхгофа
1.4. Метод контурних струмів
2. Багатополюсні елементи електричних схем
3. Особливості формування математичних моделей електричних схем з багатополюсниками
Зміст книги
- 1. Математичні моделі електричних схем з двополюсниками
- 2. Повна система рівнянь електричної схеми
- 3. Формулювання законів Кірхгофа
- 4. Метод вузлових напруг
- 5. Метод контурних струмів
- 6. Багатополюсні елементи електричних схем
- 7. Особливості формування математичних моделей електричних схем з багатополюсниками
1. Математичні моделі електричних схем з двополюсниками
Електрична схема, як і будь-яка динамічна система характеризується певною сукупністю змінних, які визначають її стан. Як такі змінні найчастіше використовують струми та напруги окремих елементів схеми. Для математичного опису процесів в електричних колах необхідно утворити сукупність рівнянь, які б відображали взаємозалежності між змінними, що характеризують електричний стан кола. Таку сукупність рівнянь називають математичною моделлю електричного кола.
Рівняння, які утворюють математичну модель електричного кола, діляться на дві групи, перша з яких зумовлена взаємозв’язком струмів та напруг на окремих елементах схеми, а друга визначається способом з’єднання елементів у схемі. Рівняння першого типу називаються компонентними рівняннями, а другого – топологічними.
2. Повна система рівнянь електричної схеми
Вузли та контури електричної схеми визначають спосіб з’єднання компонент схеми.
Розглянемо електричну схему, яка складається з n елементів. Кількість змінних, які характеризують електричний стан такої схеми, очевидно, дорівнює 2n, бо кожний двополюсний елемент характеризується струмом та напругою. Оскільки струми та напруги на кожному з елементів пов’язані відповідними співвідношеннями, їх можна записати у такому узагальненому вигляді:
![]() (2.11)
(2.11)
Сукупність виразів (2.11) утворює систему компонентних рівнянь електричної схеми, розмір якої, очевидно, дорівнює n. Наступні n рівнянь, необхідних для побудови математичної моделі схеми, визначимо із залежностей, зумовлених з’єднанням елементів у схему, тобто топологічних.
В електротехніці топологічні залежності визначаються законами Кірхгофа, для формування яких введемо деякі означення.
Вузлом електричної схеми називають місце з’єднання трьох або більше елементів схеми.
Контуром електричної схеми називають замкнуту послідовність, складену з елементів схеми.
Системою незалежних контурів електричної схеми називають сукупність контурів, кожен з яких відрізняється від інших хоча б одним елементом.
3. Формулювання законів Кірхгофа
Перший закон Кірхгофа Алгебрична сума струмів елементів схеми, які утворюють вузол, дорівнює нулеві. Струми, які входять у вузол, беруться із знаком плюс, а ті, що виходять – із знаком мінус.
Математичний запис першого закону Кірхгофа має такий вигляд
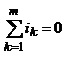 . (2.12)
. (2.12)
Повна система рівнянь електричного кола

Другий закон Кірхгофа Алгебрична сума напруг елементів схеми, які утворюють контур, дорівнює нулеві. Напруги, які збігаються з вибраним додатним напрямком обходу контуру, входять у суму із знаком “+”, а які не збігаються – беруться із знаком “-“.
Математичний запис другого закону Кірхгофа такий
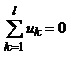 . (2.13)
. (2.13)
Якщо записати рівняння (2.12) для усіх вузлів, крім одного, а рівняння (2.13) для всіх незалежних контурів, то вони разом з системою рівнянь (2.11) утворять математичну модель електричної схеми у вигляді повної системи рівнянь, в якій кількість рівнянь і невідомих дорівнює 2n.
Як бачимо, сформувати повну систему рівнянь електричної схеми доволі просто, однак така модель має істотний недолік, зумовлений великим розміром цієї системи.
Приклад 2.1 Сформуємо повну систему рівнянь електричної схеми, показаної на рис.2.12.
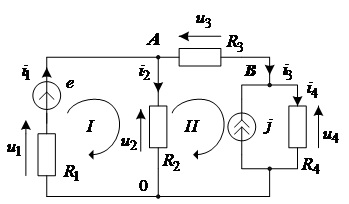
Рис.2.12. Електрична схема до прикладу 2.1
Ця схема складається із чотирьох двополюсних елементів,
тому що неідеальні джерела енергії вважаються одним елементом. Змінними, що
визначають електричний стан схеми, є така сукупність струмів та напруг ![]() Вузлів у цій схемі – три, вони позначені
великими буквами А,В,О, а контурів, що утворюють незалежну систему – два, вони
позначені римськими цифрами, біля яких показаний додатний напрямок обходу
контурів.
Вузлів у цій схемі – три, вони позначені
великими буквами А,В,О, а контурів, що утворюють незалежну систему – два, вони
позначені римськими цифрами, біля яких показаний додатний напрямок обходу
контурів.
Запишемо систему компонентних рівнянь
![]()
Розглянувши два вузли (А, В) із трьох, запишемо співвідношення між струмами елементів згідно з першим законом Кірхгофа
![]()
Контурні залежності згідно з другим законом Кірхгофа записуються так:
е![]()
Об’єднавши записані вище рівняння і виконавши елементарні перетворення, отримуємо повну систему рівнянь електричної схеми у такому вигляді:
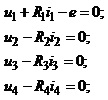
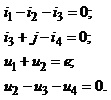
4. Метод вузлових напруг
Цей метод дає змогу будувати значно простіші математичні моделі електричних кіл за рахунок істотного зменшення кількості змінних, які характеризують їхній стан. Як змінні тут використовуються вузлові напруги, тобто різниці потенціалів між деяким вибраним вузлом для цієї схеми (базисним вузлом) та іншими вузлами. Очевидно, кількість вузлових напруг на одиницю менша за кількість вузлів схеми. Знаючи вузлові напруги схеми, легко визначити напругу на будь-якому елементі схеми, оскільки він обов’язково з’єднує якісь два вузли і тому ця напруга визначається як різниця відповідних вузлових напруг. Останнє показано на рис.2.13.
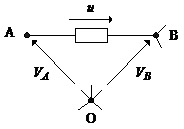
Рис.2.13. Зв’язок напруг елементів схеми з її вузловими напругами
О – базисний вузол; VA, VB – вузлові напруги вузлів А та В; u – напруга вибраного елемента схеми.
З рисунка видно, що згідно з другим законом Кірхгофа справедливим є
u=VB-VA . (2.14)
Для виведення рівнянь електричної схеми у базисі вузлових напруг допустимо, що ми розглядаємо деяку електричну схему, що складається із резисторів та джерел струму, тобто узагальненим елементом цієї схеми є неідеальне джерело струму, зображене на рис.2.11, б. Розглянемо окремий вузол (не базисний) такої схеми. Очевидно, для цього вузла справедливий перший закон Кірхгофа
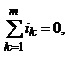
де ik – струм к-го елемента, що з’єднується одним затискачем з вибраним вузлом, який позначимо буквою А, а другим – з деякими іншими вузлами, які позначатимемо буквою з індексом Bk. Ураховуючи співвідношення (2.9б), а також (2.14), запишемо вираз для струму ik:
![]() , (2.15)
, (2.15)
де jk, gk – параметри к-го елемента схеми; VA,VB – відповідно вузлові напруги.
Перепишемо вираз для закону Кірхгофа з урахуванням (2.15). Виконавши прості перетворення, отримуємо:
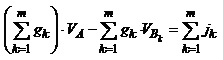 . (2.16)
. (2.16)
Записавши рівняння виду (2.16) для кожного з n-1 вузлів схеми і об’єднавши їх у систему, одержимо математичну модель схеми у вигляді системи рівнянь вузлових напруг, яку зручно записати у такому матричному вигляді:
![]() , (2.17)
, (2.17)
де ![]() – вектор-стовпчик, компонентами якого є (n-1) вузлових напруг схеми;
– вектор-стовпчик, компонентами якого є (n-1) вузлових напруг схеми; ![]() – (n-1)- вимірний
вектор, що формується із струмів ідеальних джерел струмів схеми; Y – квадратна матриця вузлових провідностей
схеми.
– (n-1)- вимірний
вектор, що формується із струмів ідеальних джерел струмів схеми; Y – квадратна матриця вузлових провідностей
схеми.
Для формування матриці Y та вектора ![]() існують прості правила; урахувавши, що кожен
рядок та стовпчик матриці Y відповідає певному вузлу схеми, сформулюємо
їх.
існують прості правила; урахувавши, що кожен
рядок та стовпчик матриці Y відповідає певному вузлу схеми, сформулюємо
їх.
Діагональні елементи матриці Y утворюються підсумуванням провідностей елементів схеми, дотичних до відповідного вузла.
Позадіагональний елемент матриці Y визначається провідністю елемента схеми, який з’єднує відповідні вузли, взяті із протилежним знаком.
Компонента вектора ![]() визначається як алгебрична сума струмів джерел
струму, що входять у відповідний вузол схеми.
визначається як алгебрична сума струмів джерел
струму, що входять у відповідний вузол схеми.
Приклад 2.2
Розглянемо
схему, показану на рис.2.14, і запишемо для неї матрицю Y і вектор ![]()
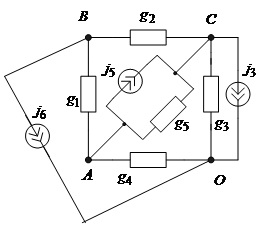
Рис.2.14. Електрична схема до прикладу 2.2
Вибравши як базисний вузол схеми вузол O згідно з наведеними вище правилами, запишемо матричні коефіцієнти рівняння вузлових напруг (2.17)
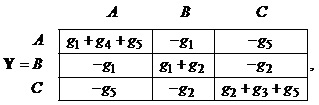
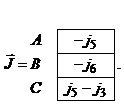
Контурні струми – це певна математична абстракція, яка дає змогу легко визначити струми реальних компонент електричного кола.
5. Метод контурних струмів
Ця математична модель використовує як змінні, що характеризують електричний стан кола, контурні струми, тобто струми, які циркулюють у деякому контурі схеми. Контурні струми і струми елементів електричної схеми пов’язані простими лінійними співвідношеннями, а саме струм будь-якого елемента схеми визначається як алгебрична сума контурних струмів контурів, у які цей елемент входить. Знак доданка у цій сумі визначається співвідношенням напрямків струмів контурів і струму цього елемента.
Зауважимо, що у цьому методі беруться до уваги контурні струми лише системи незалежних контурів.
Для виведення рівнянь контурних струмів розглянемо електричну схему, що складається з резисторів та джерел ЕРС, тобто в загальному випадку кожен елемент можна подати як неідеальне джерело ЕРС (рис.2.11, а). На підставі другого закону Кірхгофа запишемо рівняння для деякого контуру
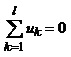
і врахувавши співвідношення (2.9а), отримаємо
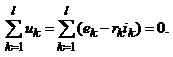 (2.18)
(2.18)
Визначимо струми окремих елементів схеми через контурні струми
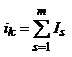 , (2.19)
, (2.19)
де Is – контурні струми контурів до складу яких входить k-й елемент схеми. Виконавши певні перестановки у рівнянні (2.18) і врахувавши співвідношення (2.19), одержимо рівняння контурних струмів для вибраного контуру у такому вигляді
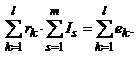 (2.20)
(2.20)
Записавши такі рівняння для всіх контурів із незалежної системи контурів, отримаємо систему рівнянь контурних струмів для розглянутої схеми, яку зручно записати у матричному вигляді
![]() , (2.21)
, (2.21)
де Z – матриця опорів системи рівнянь контурних струмів; E– вектор ЕРС контурів; I – вектор контурних струмів. Елементи матриці Z та вектор E визначаються за такими правилами.
Діагональні елементи матриці Z є сумою опорів компонентів схеми, що утворюють контур, який відповідає цьому елементу.
Позадіагональний елемент матриці Z є сумою опорів компонентів схеми, які є спільними для двох контурів, що відповідають цьому елементу, причому ця сума береться із знаком “+”, якщо напрямки обходів контурів у спільних елементах схеми збігаються і “–” коли вони є протилежними.
Компоненти вектора E дорівнюють алгебричній сумі ЕРС джерел, які входять у відповідний контур.
Приклад 2.3 Складемо рівняння контурних струмів для такої схеми.
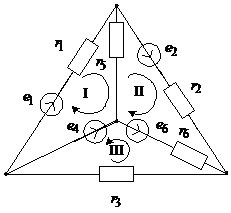
Рис.2.15. Схема до прикладу 2.3
Систему незалежних контурів цієї схеми утворюють три контури, позначені римськими цифрами. Додатні напрямки обходу контурів показані на рис.2.15. Запишемо матрицю Z та вектор E для цієї схеми згідно з наведеними вище правилами.
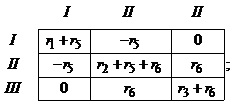
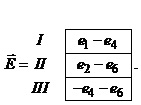
Навпроти
рядків та стовпчиків матриці Z та вектора ![]() вказані відповідні контури.
вказані відповідні контури.
6. Багатополюсні елементи електричних схем
У сучасних електронних колах поряд із компонентами, які мають два затискачі (двополюсники), використовуються і компоненти, які мають більше від двох затискачів для під’єднання їх до зовнішнього кола. Наприклад, це можуть бути транзистори, інтегральні схеми тощо. Такі елементи називаються багатополюсними елементами, або багатополюсниками.
Схемне зображення багатополюсника показано на рис.2.16.
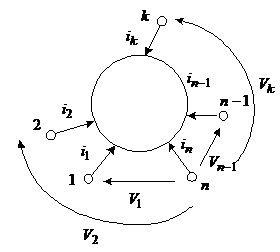
Рис.2.16. Схемне зображення багатополюсника
Схемний елемент, зображений на рис.2.16, називають багатополюсником або, конкретніше, n-полюсником, а його виводи – полюсами. На цьому самому рисунку показано полюсні струми та напруги такого багатополюсника. Як бачимо, полюсні напруги – це не що інше, як вузлові напруги, визначені стосовно деякого вибраного полюса багатополюсника (у цьому разі полюса n). Тобто кількість полюсних напруг у n - полюсника дорівнює n-1, незалежних струмів у n– полюснику є теж n-1, оскільки струм базисного полюса згідно з першим законом Кірхгофа можна виразити через інші полюсні струми багатополюсника
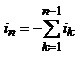 (2.22)
(2.22)
Очевидно, між струмами та напругами багатополюсника існує взаємозв’язок, який зручно записувати у вигляді таких матричних рівнянь
а)![]() б)
б)![]() (2.23)
(2.23)
де ![]() ; i– вектор
полюсних струмів багатополюсника;
; i– вектор
полюсних струмів багатополюсника; ![]() – вектор
полюсних напруг; j– вектор
струмів внутрішніх джерел багатополюсника;E– вектор ЕРС
внутрішніх джерел багатополюсника; Y– матриця
провідностей багатополюсника, Z – матриця опорів багатополюсника.
– вектор
полюсних напруг; j– вектор
струмів внутрішніх джерел багатополюсника;E– вектор ЕРС
внутрішніх джерел багатополюсника; Y– матриця
провідностей багатополюсника, Z – матриця опорів багатополюсника.
Рівняння (2.23а) – називають рівнянням
багатополюсника в Y–параметрах, а рівняння (2.23б) – рівнянням багатополюсника в Z– параметрах. Очевидно, обидва рівняння пов’язані, зокрема ![]() . Діагональні
елементи матриці Y(Z) називають власними провідностями (опорами)
полюсів, а позадіагональні – взаємними провідностями (опорами).
. Діагональні
елементи матриці Y(Z) називають власними провідностями (опорами)
полюсів, а позадіагональні – взаємними провідностями (опорами).
Доволі часто у теорії кіл окремо розглядають спеціальний тип багатополюсників, які називають прохідними чотириполюсниками (рис.2.17).

Рис.2.17. Зображення прохідного чотириполюсника
Оскільки у прохідному
чотириполюснику обов’язковими є умови ![]() , то такий багатополюсник
характеризується лише чотирма струмами та напругами, зокрема,
, то такий багатополюсник
характеризується лише чотирма струмами та напругами, зокрема, ![]() – вхідний струм
і напруга відповідно,
– вхідний струм
і напруга відповідно, ![]() – вихідні струм
і напруга.
– вихідні струм
і напруга.
Прохідними чотириполюсниками зручно зображати такі пристрої електронних схем, як фільтри, підсилювачі, випрямлячі тощо.
Будемо розглядати лише пасивні чотириполюсники, тобто такі прохідні чотириполюсники, які не містять джерел енергії. Для таких чотириполюсників запишемо рівняння у різних формах.
а) рівняння прохідного чотириполюсника в Y– параметрах
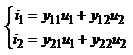 ; (2.24)
; (2.24)
б) рівняння прохідного чотириполюсника в Z– параметрах
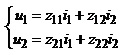 ; (2.25)
; (2.25)
в) рівняння прохідного чотириполюсника у гібридних параметрах
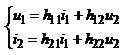 ; (2.26)
; (2.26)
г) рівняння прохідного чотириполюсника в а – параметрах
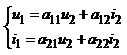 . (2.27)
. (2.27)
Зауважимо, що рівняння (2.26) часто використовують для опису таких компонент електронних кіл, як біполярні транзистори, а рівняння (2.27) зручні для опису класичних LC – фільтрів та процесів у довгій лінії.
На прикладі рівнянь чотириполюсника в а – параметрах покажемо, як можна інтерпретувати конкретні параметри чотириполюсника. З рівняння (2.27) можна записати такі співвідношення:
а)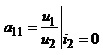 ; б)
; б)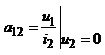 ;
;
с)
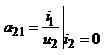 ; д)
; д)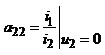 . ( 2.28)
. ( 2.28)
Із поданих співвідношень випливає, що коефіцієнт a11 можна трактувати як обернене значення коефіцієнта передавання напруги чотириполюсника із входу на вихід за неробочого режиму на виході.
Аналогічно коефіцієнт a22 є оберненим значенням коефіцієнта передавання струму при короткому замиканні вихідних затискачів чотириполюсника.
Водночас коефіцієнт a12 є відповідним передавальним опором для режиму короткого замикання, а a21 – передавальною провідністю для неробочого ходу на виході.
Коефіцієнти рівнянь (2.24) – (2.27) – тобто параметри чотириполюсника взаємозв’язані і цей зв’язок легко знайти за допомогою простих алгебричних перетворень.
Доволі часто для характеристики прохідних чотириполюсників використовують такі параметри, як коефіцієнти передавання:
![]() – коефіцієнт передавання напруги;
– коефіцієнт передавання напруги;
![]() – коефіцієнт передавання струму.
– коефіцієнт передавання струму.
7. Особливості формування математичних моделей електричних схем з багатополюсниками
Під час формування математичних моделей схем з багатополюсниками виникають певні особливості і тому наведені в п. 2.3 правила формування рівнянь необхідно узагальнити. Для прикладу розглянемо формування рівняння вузлових напруг електричної схеми, в якій є один багатополюсник. У такому разі зручно використовувати для його опису математичну модель у вигляді рівняння в Y– параметрах (2.43а). Також як базисний вузол схеми рекомендується вибирати вузол, до якого приєднаний базисний полюс багатополюсника. У разі виконання вказаних умов правила формування елементів матриці Y та вектора J (§2.3.2) узагальнюються так.
Діагональні елементи матриці вузлових провідностей є сумою провідностей двополюсних елементів схеми та власних провідностей полюсів багатополюсника, які утворюють відповідний вузол.
Позадіагональні елементи матриці вузлових провідностей дорівнюють сумі провідностей двополюсних елементів схеми, які з’єднують відповідні вузли схеми, взятій із протилежним знаком, та взаємних провідностей багатополюсника полюсів, дотичних до вказаних вузлів.
Компоненти вектора J є алгебричною сумою струму джерел струмів, а також відповідних компонент вектора струмів J багатополюсника.
Приклад 2.4. Запишемо рівняння вузлових напруг для схеми, зображеної на рисунку.
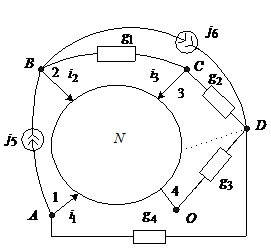
Рис.2.18. Електрична схема до прикладу 2.4
Рівняння чотириполюсника, показаного на схемі, запишемо у такому вигляді
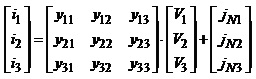
Вузол О вибираємо як базисний, а відповідно для полюсних напруг вузлів A,B,C,D запишемо матрицю Y та вектор J.
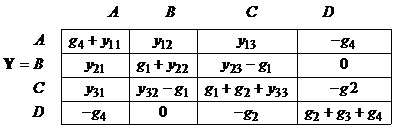
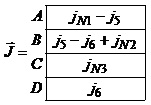 .
.
Подібно можна формувати рівняння вузлових напруг схем із декількома багатополюсниками, базисні вузли яких під’єднуються до одного вузла.