Тема 3. Математичні моделі електричних схем
Математичні моделі електричних схем
1. Математичні моделі електричних схем з двополюсниками1.1. Повна система рівнянь електричної схеми
1.3. Метод вузлових напруг
1.2. Формулювання законів Кірхгофа
1.4. Метод контурних струмів
2. Багатополюсні елементи електричних схем
3. Особливості формування математичних моделей електричних схем з багатополюсниками
4. Метод вузлових напруг
Цей метод дає змогу будувати значно простіші математичні моделі електричних кіл за рахунок істотного зменшення кількості змінних, які характеризують їхній стан. Як змінні тут використовуються вузлові напруги, тобто різниці потенціалів між деяким вибраним вузлом для цієї схеми (базисним вузлом) та іншими вузлами. Очевидно, кількість вузлових напруг на одиницю менша за кількість вузлів схеми. Знаючи вузлові напруги схеми, легко визначити напругу на будь-якому елементі схеми, оскільки він обов’язково з’єднує якісь два вузли і тому ця напруга визначається як різниця відповідних вузлових напруг. Останнє показано на рис.2.13.
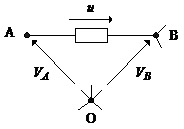
Рис.2.13. Зв’язок напруг елементів схеми з її вузловими напругами
О – базисний вузол; VA, VB – вузлові напруги вузлів А та В; u – напруга вибраного елемента схеми.
З рисунка видно, що згідно з другим законом Кірхгофа справедливим є
u=VB-VA . (2.14)
Для виведення рівнянь електричної схеми у базисі вузлових напруг допустимо, що ми розглядаємо деяку електричну схему, що складається із резисторів та джерел струму, тобто узагальненим елементом цієї схеми є неідеальне джерело струму, зображене на рис.2.11, б. Розглянемо окремий вузол (не базисний) такої схеми. Очевидно, для цього вузла справедливий перший закон Кірхгофа
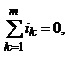
де ik – струм к-го елемента, що з’єднується одним затискачем з вибраним вузлом, який позначимо буквою А, а другим – з деякими іншими вузлами, які позначатимемо буквою з індексом Bk. Ураховуючи співвідношення (2.9б), а також (2.14), запишемо вираз для струму ik:
![]() , (2.15)
, (2.15)
де jk, gk – параметри к-го елемента схеми; VA,VB – відповідно вузлові напруги.
Перепишемо вираз для закону Кірхгофа з урахуванням (2.15). Виконавши прості перетворення, отримуємо:
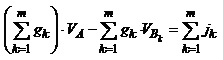 . (2.16)
. (2.16)
Записавши рівняння виду (2.16) для кожного з n-1 вузлів схеми і об’єднавши їх у систему, одержимо математичну модель схеми у вигляді системи рівнянь вузлових напруг, яку зручно записати у такому матричному вигляді:
![]() , (2.17)
, (2.17)
де ![]() – вектор-стовпчик, компонентами якого є (n-1) вузлових напруг схеми;
– вектор-стовпчик, компонентами якого є (n-1) вузлових напруг схеми; ![]() – (n-1)- вимірний
вектор, що формується із струмів ідеальних джерел струмів схеми; Y – квадратна матриця вузлових провідностей
схеми.
– (n-1)- вимірний
вектор, що формується із струмів ідеальних джерел струмів схеми; Y – квадратна матриця вузлових провідностей
схеми.
Для формування матриці Y та вектора ![]() існують прості правила; урахувавши, що кожен
рядок та стовпчик матриці Y відповідає певному вузлу схеми, сформулюємо
їх.
існують прості правила; урахувавши, що кожен
рядок та стовпчик матриці Y відповідає певному вузлу схеми, сформулюємо
їх.
Діагональні елементи матриці Y утворюються підсумуванням провідностей елементів схеми, дотичних до відповідного вузла.
Позадіагональний елемент матриці Y визначається провідністю елемента схеми, який з’єднує відповідні вузли, взяті із протилежним знаком.
Компонента вектора ![]() визначається як алгебрична сума струмів джерел
струму, що входять у відповідний вузол схеми.
визначається як алгебрична сума струмів джерел
струму, що входять у відповідний вузол схеми.
Приклад 2.2
Розглянемо
схему, показану на рис.2.14, і запишемо для неї матрицю Y і вектор ![]()
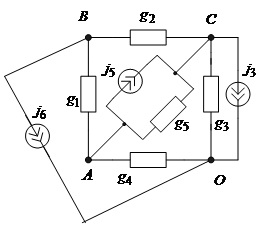
Рис.2.14. Електрична схема до прикладу 2.2
Вибравши як базисний вузол схеми вузол O згідно з наведеними вище правилами, запишемо матричні коефіцієнти рівняння вузлових напруг (2.17)
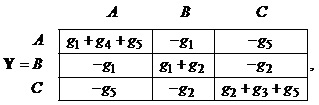
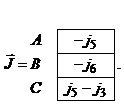
Контурні струми – це певна математична абстракція, яка дає змогу легко визначити струми реальних компонент електричного кола.