Тема 1. Основні поняття теорії сигналів

Проходження сигналів в електронних колах супроводжується різноманітними перетвореннями їхніх характеристик. У випадкових сигналів можуть змінюватися закони їхнього розподілу, аналітичний розрахунок яких дуже складний. Проте виявляється, що значно простішим є розрахунок певних числових характеристик законів розподілу, які можна визначити на підставі нескладних експериментів. У багатьох випадках точність розрахунків, яку забезпечують згадані числові характеристики, цілком достатня для потреб практики. Такими числовими характеристиками є моменти випадкової величини. Вони є детермінованими числами.

                Момент n-го порядку M_n(x) неперервної випадкової величини х визначають за формулою:

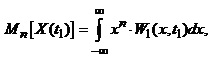                                                           (1.65)

де W₁(x,t₁) – одновимірна густина розподілу ймовірностей випадкової величини x(t₁).

                Математичним сподіванням або середнім значенням випадкової величини  називають момент першого порядку:

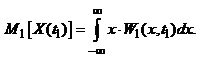                                                         (1.66)

Усереднення випадкової величини x(t₁) згідно з (1.66) здійснюють за ансамблем реалізацій. Тому за наявності ансамблю із N реалізацій випадкового процесу статистичне визначення його середнього значення у перетині в момент часу t_k здійснюємо за формулою:

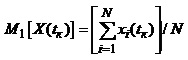                                                      (1.67)

                Взаємозв’язок між формою закону розподілу ймовірностей та його числовими характеристиками стає наочнішим у разі використання поняття центрованої випадкової величини. Випадкова величина називається центрованою, якщо її середнє значення дорівнює нулеві. Отже, випадкова величина X(t_к) центрується відніманням від неї середнього значення M₁[X(t_к)]:

                           .                               (1.68)

                На відміну від початкових моментів, які визначають за формулою (1.65), моменти центрованої величини називають центральними моментами. Центральний момент n-го порядку розраховують за формулою:

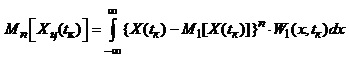      .            (1.69)

                Центральний момент першого порядку M₁[X_ц(t_k)] за означенням дорівнює нулеві.

                Центральний момент другого порядку

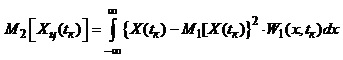                         (1.70)

Цей момент характеризує розсіювання можливих значень випадкової величини X(t_k) стосовно її середнього значення і називається дисперсією. Часто використовують таке позначення дисперсії:s²[X(t_к)]. Величину s[X(t_к)], що дорівнює додатному значенню кореня квадратного з центрального моменту другого порядку, називають середнім квадратичним відхиленням випадкової величини X(t_к).

                На підставі ансамблю з N реалізацій випадкового процесу статистичне визначення дисперсії виконуємо за формулою:

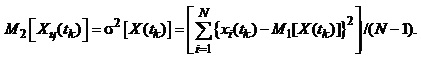      (1.71)

                Розв’язуючи багато практичних задач, доводиться виконувати арифметичні операції над випадковими сигналами. При цьому числові характеристики результуючих сигналів достатньо просто визначають через числові характеристики первинних сигналів. Наприклад, якщо Х₁(t) та Х₂(t) є первинними   незалежними сигналами, а А – постійна величина, то справедливі такі співвідношення:

                 

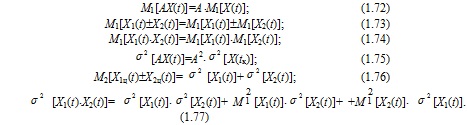
Подані співвідношення можна узагальнити для більшої кількості випадкових сигналів.

                Загалом числові характеристики одновимірних розподілів залежать від часу. Це зумовлюється часовою залежністю функції розподілу F₁(x,t) та густини розподілу W₁(x,t). У такому разі числові характеристики замість чисел стають функціями часу і їх називають моментними функціями.

                Повніше можна описати випадковий процес, якщо визначити взаємозв’язок між його значеннями при двох і більше моментах часу. Такий взаємозв’язок описують n-вимірна функція розподілу ймовірностей F_n(x₁, t₁; x₂, t₂; ... x_n, t_n) та n-вимірна густина розподілу ймовірностей W_n(x₁, t₁; x₂, t₂; ...x_n, t_n). Очевидно, що чим більше значення n, тим точніше описуємо випадковий процес.

                Зауважимо, що для великих значень n аналітичний опис функцій F_n (ּ) та W_n(ּ) дуже складний і практично дуже важко отримати його. Проте існують деякі типи випадкових процесів, властивості яких можна повністю описати за допомогою густини розподілу ймовірностей для скінченного значення n. Такими процесами є білий шум та марковські випадкові процеси.

                Білий шум характеризується тим, що його миттєві значення у різні моменти часу є незалежними. Отже, n -вимірну густину розподілу білого шуму повністю визначаємо добутком n одновимірних густин.

Марковські випадкові процеси характеризуються тим, що густина розподілу ймовірностей у момент t_i залежить лише від значення випадкового процесу в попередній момент часу і не залежить від більш ранніх подій. Відповідний аналіз показує, що n-вимірну густину розподілу ймовірностей випадкового марковського процесу можна описати за допомогою густин розподілу ймовірностей, не вищих від другого порядку.

                Закінчуючи розгляд основних характеристик випадкових сигналів, зазначимо, що множину випадкових процесів можна поділити на дві великі групи: стаціонарні та ергодичні.

                Випадковий процес X(t) є стаціонарним, якщо будь-яка n-вимірна функція розподілу ймовірностей його значень, узятих у різні моменти часу, не змінюється за будь-якого зсуву (зміщення) цих моментів уздовж осі часу. Стаціонарні випадкові процеси виникають у джерелах випадкових сигналів за усталених режимів роботи, за незмінних умов зовнішнього середовища та незмінних значень параметрів електронних кіл, через які проходять випадкові сигнали.

                Ергодичні випадкові процеси характерні тим, що їхні закони розподілу можна визначити, усереднюючи необхідні величини на підставі лише однієї реалізації, отриманої за достатньо великий проміжок часу. Це означає, що для ергодичних стаціонарних процесів усереднення за ансамблем реалізацій та усереднення в часі в межах одної реалізації дають однаковий результат.