Тема 1. Основні поняття теорії сигналів

                Оскільки характер прийнятих сигналів як носіїв інформації на приймальному пункті заздалегідь не є відомим, то з цього погляду сигнали треба розглядати як випадкові функції часу.

                Отже, математичною моделлю випадкового сигналу є випадкова функція часу.

                Випадкова функція будь-якого аргументу – це така функція, значення якої для кожного значення аргументу випадкове. Випадкову функцію часу називають випадковим процесом. Позначимо його функцією X(t).

                Спостерігаючи багаторазово за одним і тим самим випадковим процесом, що перебігає в незмінних умовах, кожен раз отримуємо конкретні реалізації x(t), не подібні одна на одну, проте на підставі такого спостереження можна виявити певні закономірності, що характеризують цей процес, та визначити сукупність невипадкових числових характеристик, які описують його. Випадковий процес повністю характеризується нескінченно великою кількістю реалізацій, які утворюють ансамбль реалізацій.

                Розглянемо N реалізацій випадкового процесу X(t) (рис.1.14).

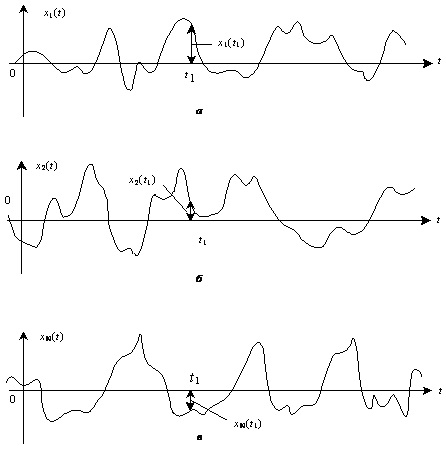
Рис.1.14. Ансамбль реалізацій випадкового процесу

                Сукупність миттєвих значень випадкового процесу, заданого ансамблем реалізацій у довільний момент часу, називають перетином випадкового процесу.

                На рис.1.14 показано перетин випадкового процесу X(t) у момент t₁, який дає змогу визначити сукупність миттєвих значень процесу x₁(t₁), x₂(t₁), ...x_N(t₁), яку можна розглядати як сукупність значень деякої випадкової величини X(t₁).

                Ця сукупність дає можливість визначити одновимірну функцію розподілу ймовірностей випадкової величини X(t₁). Для цього виділимо ті значення, які в момент часу t₁ задовольняють умову:

                                                 X(t₁)<x₁,                                                 (1.56)

де x₁ – деяке вибране значення випадкового процесу.

                Позначимо кількість цих значень як n(x₁, t₁). Відношення n(x₁, t₁)/N називають у теорії ймовірностей частотою настання події. У такому разі під подією розуміємо виконання умови (1.56). За достатньо великого значення N відношення n(x₁, t₁)/N прямуватиме до постійного числа, яке називають ймовірністю того, що при t=t₁ випадкова функція X(t) менша від значення x₁:

 

                                                  (1.57)

                Діючи аналогічно для інших значень x в інтервалі -¥ £ x £ ¥, можемо побудувати одновимірну функцію розподілу ймовірностей випадкового процесу:

                                       F₁(x, t₁)=P{X(t₁)<x}.                                       (1.58)

Функція  матиме ступінчатий характер тоді, коли випадковий процес набуває дискретних значень. Якщо ж випадковий процес змінює свої значення неперервно, то функція F₁(x, t₁) теж матиме вигляд плавної кривої. Зауважимо, що функція розподілу ймовірностей є неспадною функцією свого аргументу, що випливає з її означення.

                Тісно пов’язаною з одновимірною функцією розподілу ймовірностей випадкового процесу є одновимірна густина розподілу ймовірностей випадкового процесу, яку на підставі ансамблю реалізацій наближено визначають так:

                            ,                             (1.59)

де n(x+Dx, t₁) – кількість реалізацій, значення яких у момент t₁ були менші від x+Dx, а n(x,t₁) визначаємо, як і раніше.

                За такого визначення густина розподілу теж має ступінчатий вигляд. Підвищення точності визначення густини розподілу досягають зменшенням інтервалу  Dx до нуля:

                     .                      (1.60)

                Із (1.60) випливає, що густина розподілу є похідною одновимірної функції розподілу:

                                                                      (1.61)

                З іншого боку отримуємо:

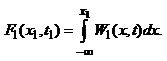                                                                      (1.62)

                Очевидно, що ймовірність перебування випадкової функції X(t) у момент t₁ в інтервалі між x₁ та x₂, дорівнює:

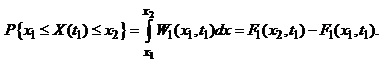            (1.63)

Зрозуміло, що ймовірність перебування значення випадкового процесу у межах від -¥ до ¥, дорівнює одиниці:

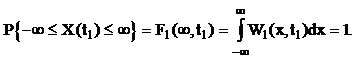                      (1.64)

 Інтегральний та диференціальний закони розподілу ймовірностей дають змогу визначити у довільний момент часу ймовірність перебування значення випадкової величини у заданих межах.

                Зауважимо, що функції F₁(x, t) та W₁(x,t) для довільних значень x та t завжди набувають додатні значення.

                Часто функцію розподілу ймовірностей F₁(x,t)  називають інтегральним законом розподілу, а густину розподілу ймовірностей – диференціальним законом розподілу ймовіростей.

                Функції F₁(x, t₁) та W₁(x,t₁) статистично повністю характеризують значення випадкового процесу X(t) у заданий момент часу t₁ і тому їх називають одновимірними. Ці функції є найпростішими характеристиками випадкового процесу, оскільки вони дають уявлення про процес лише в окремі фіксовані моменти часу.