Тема 1. Основні поняття теорії сигналів

Особливістю розглянутих раніше аналогових сигналів є те, що сукупність їхніх миттєвих значень на довільному часовому інтервалі описується неперервною (нескінченною) множиною точок, кожна з яких відображає миттєве значення сигналу у відповідний момент часу і може набувати неперервну (нескінченну) множину значень. Отже, уся множина точок містить у собі нескінченну кількість інформації, тому вона часто малопридатна для сприйняття, аналізу та ефективного оброблення і потребує стискання первинної інформації без істотної втрати  корисної інформації.

                Перетворення аналогового сигналу в дискретний у часі чи цифровий сигнал еквівалентне поданню його скінченною множиною точок, що полегшує зберігання та оброблення інформації, дає змогу збільшувати кількість сигналів, які поширюються по одному й тому самому каналу зв’язку (ущільнювати канали зв’язку), стискати первинну інформацію тощо.

            Дискретизацією називають таке перетворення аналогового сигналу s(t), за якого його описують множиною миттєвих значень s(t_i) у фіксовані моменти часу t₁, t₂, ...t_n (рис.1.6)

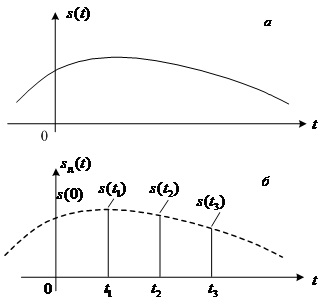
Рис.1.6. Дискретизація аналогового сигналу

                Миттєві значення s(t_i) дискретизованого сигналу називають відліками, а часовий інтервал Dt= t_i-t_i-1=T₀ між двома сусідніми відліками – інтервалом дискретизації. Очевидно, що збільшення інтервалу дискретизації збільшує пропускну здатність каналу зв’язку, але одночасно збільшує і похибку відтворення первинного сигналу s(t). Тому інтервали дискретизації вибирають з урахуванням того, щоб на підставі наявних відліків s(t_i) можна відтворити із заданою точністю первинну функцію s(t) на приймальному пункті.

Здебільшого для сигналів, які утворюються у джерелах інформації, характерні порівняно повільні зміни в часі миттєвих значень та велика тривалість. Аналіз спектральних властивостей таких сигналів показує, що їхній спектральний склад здебільшого зосереджується в обмеженій смузі частот 0...w_в, а спектральні складові з частотами, вищими від w_в, практично відсутні. Такі сигнали прийнято називати сигналами з обмеженим спектром. Саме ця властивість дає змогу замінити, а відтак знову відновити із заданою точністю неперервний сигнал, заданий скінченною множиною відліків, узятих у дискретні моменти часу.

              Умови вибору інтервалу дискретизації сигналу з обмеженим спектром визначає теорема відліків (теорема Котельникова – Шеннона).

                Умови вибору інтервалу дискретизації Dt, який забезпечує відновлення із заданою точністю первинного аналогового  сигналу s(t), формулює теорема відліків (теорема Котельникова – Шеннона): неперервний сигнал s(t), у спектрі якого відсутні частоти, вищі від w_в, повністю визначається послідовністю своїх миттєвих значень, узятих через інтервал часу Dt£p/w_в, і може бути поданий рядом:

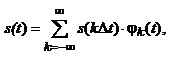                                                                   (1.32)

в якому базисні функції мають вигляд:

                                j_k(t)=sin[w_в(t-kDt)]/[w_в(t-kDt)]                               (1.33)

            Ряд (1.32) відомий як ряд Котельникова. Він дає змогу визначити первинний сигнал у довільний момент часу на підставі відліків його миттєвих значень, які слугують ваговими коефіцієнтами при базисних функціях.

            Базисні функції мають таку властивість:

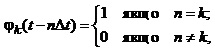
де n – ціле додатне або від’ємне число.

            На рис.1.7 зображено графіки базисних функцій для різних значень k, звідки бачимо, що кожна базисна функція j_k(t) зсунута стосовно найближчої сусідньої функції j_k-1(t) або j_k+1(t) на час , який відповідає інтервалові дискретизації Dt .

 

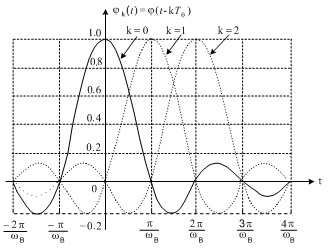
 Рис.1.7. Графіки базисних функцій j(t-kT₀)

        Відновлення аналогового сигналу s(t) на підставі ряду (1.32) зображено на рис.1.8, звідки бачимо, що точні значення сигналу s(t) отримуємо в точках відліку ....-2T₀, - T₀, 0, T₀, 2T₀  і т.д. Між точками відліку сигнал визначається точно лише тоді, коли додаються усі члени ряду, кількість яких нескінченно велика.

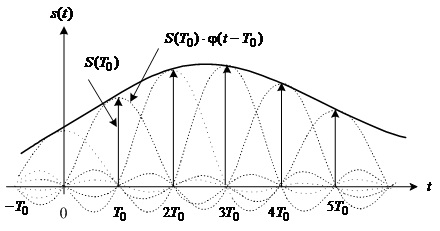
 Рис.1.8. Відновлення аналогового сигналу на підставі послідовності відліків

                Якщо неперервний в часі сигнал s(t) з найвищою частотою спектра w_в подати через ряд (1.32) на деякому обмеженому інтервалі Т_с, то кількість відліків N дорівнюватиме: N=T_c/Dt=T_cw_в/p. Цю кількість відліків називають кількістю ступенів свободи сигналу s(t), або базою сигналу. У такому разі сигнал наближено описують рядом, який складається із скінченної кількості членів, і він відтворюється точно лише в точках відліку kDt. У проміжках між відліками з’являється похибка апроксимації, яка збільшується біля країв інтервалу Т_с, де відкинуті члени ряду мають найбільше значення.

                Математичну модель дискретизоваого сигналу можна подати у вигляді добутку первинного неперервного аналогового сигналу s(t) і періодичної послідовності -імпульсів:

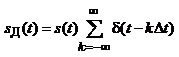                               .                                 (1.34)

                Для спектрального опису дискретизованого сигналу  застосовують до функції (1.34) пряме перетворення Фур’є.

                Пропускаючи відповідні математичні викладки, зазначимо, що модуль спектральної функції G_д(w) дискретизованого сигналу s_д(t) має вигляд модуля спектральної функції G(w) первинного неперервного аналогового сигналу і повторюється з частотою дискретизації w₀=2p/Dt=2w_в. Формування модуля спектральної функції G_д(w) дискретизованого сигналу показано на рис.1.9.

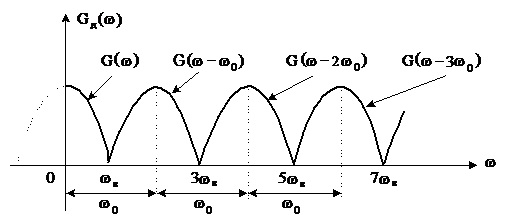
 Рис.1.9. Модуль спектральної функції G_д(w) дискретизованого сигналу

                На практиці частоту дискретизації w_Д вибирають дещо вищою, ніж 2w_в (тобто Dt<p/w_в), оскільки у такому разі сусідні спектри не перекриваються між собою, що випливає із рис.1.9. Тоді можна відтворити первинний сигнал із дискретизованого, виділивши перший пелюсток спектра за допомогою фільтра нижніх частот.

                Практично важливим є питання спектрального опису дискретизованого сигналу s_д(t), який заданий на часовому інтервалі [0, Т_с] своїми відліками s(0), s(Dt), s(2Dt), ...s((N-1)Dt). Загальна кількість відліків дорівнює N=T_c/Dt. Спектральний опис такого сигналу ґрунтується на припущенні, що сигнал s_д(t) є періодичним з періодом Т_с, тому застосовують його розклад у ряд Фур’є і знаходять відповідні амплітудні коефіцієнти.

                Часовий опис дискретизованого сигналу має вигляд:

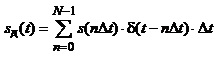                                                   (1.35)

                Комплексний ряд Фур’є такого сигналу описує формула:

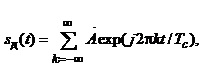                                                     (1.36)

де комплексні амплітуди визначаємо за формулою:

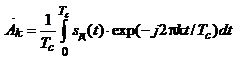                                                    (1.37)

                Підставивши вираз (1.35) в (1.37) та враховуючи фільтрувальну властивість дельта-імпульсу, отримуємо:

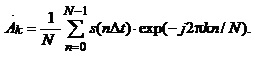                                                (1.38)

Формулу (1.38) називають дискретним перетворенням Фур’є (ДПФ) розглянутого сигналу. Вона визначає сукупність коефіцієнтів ряду Фур’є, які утворюють спектр дискретизованого сигналу.

                Аналіз властивостей ДПФ показує, що кількість різних комплексних амплітуд (крім постійної складової), які можна визначити за формулою (1.38), дорівнює половині кількості відліків за період Т_с,тобто N/2.

Постійна складова дискретизованого сигналу дорівнює середньому арифметичному усіх відліків сигналу: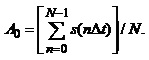

                Часто розглядають зворотну задачу дискретного спектрального аналізу: за відомими коефіцієнтами  ДПФ треба визначити відліки дискретизованого сигналу.

                Для цього у формулі (1.36) приймають t=nDt і підсумовують скінченну кількість членів ряду, які відповідають гармонікам, що входять до ряду.

                Отже, відліки дискретизованого сигналу визначають за формулою:

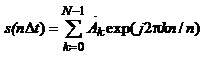                                                             (1.39)

яка описує зворотне (обернене) дискретне перетворення Фур’є.

                Дискретні перетворення Фур’є широко застосовують, використовуючи цифрові сигнали для подання та оброблення різноманітної інформації.

                Цифрові сигнали – це дискретизовані у часі та квантовані за рівнем сигнали. Кожен з рівнів подається, як правило, у вигляді n - розрядного двійкового числа:

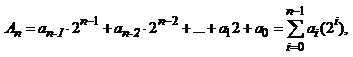                     (1.40)

де а_і –  цифра в і-му розряді двійкового числа, яка може набувати значення 0 або 1.

                Множник 2^і відіграє роль вагового коефіцієнта. Отже, двійкові числа подають у вигляді комбінацій нулів та одиниць, які відповідають значенням цифр у відповідних розрядах.

                В електричному цифровому сигналі роль “нулів” та “одиниць” відіграють звичайно сигнали напруги, які можуть бути сформовані за двома принципами:

                а) додатної логіки – коли логічній “одиниці” відповідає високе значення потенціалу, а логічному “нулеві” – низьке;

                б) від’ємної логіки – коли логічній “одиниці” відповідає низьке значення потенціалу, а логічному “нулеві” – високе.

                        Значення потенціалів, що відповідають “нулеві” та одиниці”, називають стандартними значеннями логічних сигналів.

                Із сказаного випливає, що цифровий сигнал – це послідовність комбінацій стандартних значень логічних сигналів, які утворюють n-розрядний цифровий код. Зауважимо, що стандартні сигнали відповідних розрядів можуть з’являтись одночасно (паралельний код) або послідовно (послідовний код).

                        Найпоширеніший спосіб перетворення аналогового сигналу на цифровий полягає у дискретизації аналогового сигналу в часі та у квантуванні відліків за рівнем. Питання дискретизації аналогових сигналів розглянуто раніше, тому далі коротко зупинимось на особливостях  квантування за рівнем.

                При квантуванні сигналу за рівнем неперервна множина значень аналогового сигналу s(t) замінюється множиною дискретних значень. Враховуючи це, вибирають у заданому діапазоні значень s_min...s_max  скінченну кількість дискретних значень (дискретних рівнів) і в моменти відліків t_k=kDt значення сигналу s(kDt) замінюється найближчим дискретним значенням, як показано на рис.1.10.

а

б

в

Рис.1.10. Формування цифрового сигналу

                Відстань Ds між сусідніми дискретними рівнями називають кроком квантування. Загальна кількість дискретних рівнів у заданому діапазоні значень сигналу дорівнює: . Оскільки кожному значенню дискретного рівня ставиться у відповідність певний n-розрядний двійковий код, то кількість необхідних розрядів визначають за формулою:

n ≥ log₂M  (або 2ⁿ≥M)           (1.41)

                Найчастіше двійковий код відображає двійковий номер дискретного рівня.

                Оскільки при квантуванні миттєве значення сигналу замінюється найближчим значенням  дискретного рівня, то з’являється методична (систематична) похибка, яку прийнято називати шумом квантування. Очевидно, що похибка квантування має випадковий характер, її абсолютне значення у будь-який момент часу дорівнює різниці між  квантованим значенням s_кв(t) та миттєвим значенням сигналу s(t) і не перевищує половини кроку квантування.

                Наявність методичної похибки означає, що істотною відмінністю  квантування за рівнем від  дискретизації у часі є те, що після реалізації  квантування аналоговий сигнал не можна відновити з похибкою, меншою, ніж половина кроку квантування.