5. Операторний опис сигналів

5. Операторний опис сигналів

Перетворення Лапласа як узагальнення перетворення Фур’є.

                Вище зазначалось, що спектральний опис сигналу s(t) можливий, якщо він задовольняє умову абсолютної інтегрованості. Проте чимало важливих сигналів, таких, як одиничний стрибок, гармонічне коливання та багато інших, не задовольняють цієї умови, і тому для них не можна отримати спектрального опису на підставі перетворення Фур’є. Для спектрального подання таких сигналів можна застосувати перетворення Лапласа, яке є узагальненням перетворення Фур’є і ґрунтується на використанні поняття комплексної частоти. Річ у тім, що при перетворенні Фур’є сигнал описують у вигляді суми нескінченної кількості елементарних гармонічних складових, кожна з яких змінюється у часі за законом exp(jwt).

                Примітка: нагадаємо, що згідно з відомою формулою Ейлера гармонічне коливання можна подати сумою двох експонент з уявними показниками:

cos(wt)=[exp(jwt)+exp(-jwt)]/2,

sin(wt)=[exp(jwt)-exp(-jwt)]/2j.

Зображення Лапласа дає змогу отримати спектральний опис сигналів, визначених при t³0, які не задовольняють умову абсолютної інтегрованості.

                Узагальнення перетворення Фур’є полягає в тому, що замість експоненційних сигналів з уявними показниками jw застосовують експоненційні сигнали з комплексними показниками exp(pt), де p=s+jw –  комплексне число, яке прийнято називати комплексною частотою.

                Використання поняття комплексної частоти дає змогу отримати спектральний опис сигналів, математичні моделі яких не задовольняють умову абсолютної інтегрованості. Ці сигнали повинні бути визначені при t³0, а при від’ємних значеннях t – дорівнювати нулеві. Перетворення Лапласа для таких сигналів описують виразом:

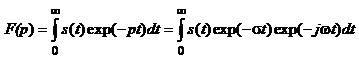                             (1.30)

                Зауважимо, що цей інтеграл існує завдяки тому, що функція s(t)×exp(-st) задовольняє умову абсолютної інтегрованості при t>0, а з іншого боку, тому, що при t<0 функція s(t)=0 (у протилежному випадку множник exp(-st) міг би призвести до розходження інтеграла).

                Сигнал s(t) називають оригіналом, а функцію F(p) – зображенням оригіналу за Лапласом (або зображенням Лапласа).

                Не наводячи доведення, зазначимо, що маючи зображення F(p), можна знайти оригінал s(t) на підставі формули:

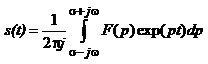                                                          (1.31)

Інтегрування в площині комплексної змінної р здійснюється уздовж нескінченної вертикальної лінії, розміщеної з правого боку від уявної осі на відстані s. Детальніше це питання розглянуто в теорії функцій комплексної змінної.

                Формули (1.30) та (1.31) називають відповідно прямим та зворотним перетворенням Лапласа.

                На практиці для знаходження оригіналів та зображень сигналів широко використовують таблиці, в яких наведено зображення за Лапласом для значної кількості оригіналів.

                Взаємну відповідність між оригіналом s(t) та його зображенням F(p) за Лапласом позначимо: s(t)¸F(p).

                Для прикладу наведемо таблицю зображень Лапласа для деяких поширених сигналів.

 Таблиця 1.1

Оригінал s(t)

Зображення F(p)

1

Множення сигналу на константу:

A×s(t)

A×F(p)

2

Диференціювання сигналу: 

p×F(p)-s(0)

3

Інтегрування сигналу:

F(p)/p

4

Зсув сигналу в часі: s(t-t0)

F(p)exp(-pt0)

5

Одиничний стрибок: 1(t)

1/p

6

Дельта-імпульс: d(t)

1

7

Гармонічні коливання (якщо t³0)

cos(wt)

sin(wt)

p/(p2+w2)

w/(p2+w2)

8

Експоненційні сигнали (якщо t³0): e±at

1/p(p+a)

                На закінчення зауважимо, що між зображенням Лапласа та спектральною функцією сигналу існує такий взаємозв’язок: якщо у виразі для зображення Лапласа замість р підставити jw, то отримуємо спектральну функцію цього сигналу.

Заміною р=jw у зображенні Лапласа отримуємо спектральну функцію G(jw) сигналу s(t).

                Операторний опис сигналів знайшов широко застосовується в аналізі процесів у лінійних електричних колах, оскільки він дає змогу звести диференціальні рівняння кола до алгебричних, записаних відносно операторних зображень сигналів, що істотно спрощує знаходження розв’язку в операторній формі. Перехід від зображення шуканого сигналу до оригіналу здійснюють, як правило, на підставі таблиць операторних зображень.