Тема 7. Основні характеристики та аналіз кіл змінного струму
1. Основні характеристики та аналіз кіл змінного струму
2. Аналіз усталених режимів кіл синусоїдного струму
3. Усталені режими електронних кіл, в яких діють несинусоїдні струми та напруги
4. Аналіз перехідних процесів електронних кіл
4.1. Класичний метод розрахунку
4.2. Операторний метод розрахунку перехідних процесів
4.3. Застосування інтеграла Дюамеля до розрахунку перехідних процесів
4.4. Числові методи розрахунку перехідних процесів електронних кіл
2. Аналіз усталених режимів кіл синусоїдного струму
Електричними колами синусоїдного струму можуть бути лише лінійні кола, оскільки будь-який нелінійний елемент кола приводить до появи струмів чи напруг, що мають несинусоїдний характер.
Враховуючи те, що частота зміни струмів та напруг у лінійних схемах є величиною постійною і визначається параметрами джерел енергії, то в усталеному режимі кожен струм чи напруга характеризується двома параметрами – амплітудою та початковою фазою. Щоб відобразити ці параметри, для гармонічних струмів та напруг вводиться поняття комплексної амплітуди синусоїдної величини
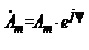 (4.21)
(4.21)
Символічний метод розрахунку дає змогу розрахувати усталені режими лінійних електричних кіл синусоїдного струму і як змінні використовує комплексні амплітуди струмів та напруг.
![]() – комплексна амплітуда синусоїдної
величини
– комплексна амплітуда синусоїдної
величини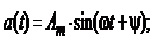 Am– амплітуда синусоїдної величини
Тобто є справедливим таке означення:
Am– амплітуда синусоїдної величини
Тобто є справедливим таке означення:
Комплексною амплітудою синусоїдної величини називають комплексне число, модуль якого дорівнює її амплітуді, а аргумент – початковій фазі.
Комплексна амплітуда однозначно описує синусоїдну величину за умови заданої частоти, тобто цю величину можна вважати комплексним зображенням змінної у часі синусоїдної величини. Замінивши у схемах реальні струми та напруги на їхні комплексні зображення (комплексні амплітуди), ми позбудемось часової залежності, що значно спрощує подальший аналіз кіл синусоїдного струму. Покажемо це на прикладах конкретних елементів електричних схем:
а) Резистор
Після підстановки у відоме співвідношення UR=RI виразу (4.14) для синусоїдного струму отримуємо
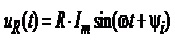 . Перейшовши у лівій і правій частинах цього виразу до комплексних амплітуд,
маємо
. Перейшовши у лівій і правій частинах цього виразу до комплексних амплітуд,
маємо
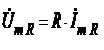 (4.22)
(4.22)
б) Котушка індуктивності
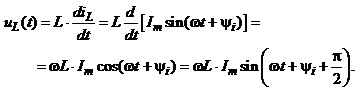
Знов-таки замінивши перший і останній вирази їхніми комплексними амплітудами, отримуємо:
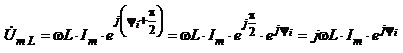 .
.
Або в остаточному вигляді
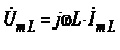 (4.23)
(4.23)
в) Конденсатор
Переходячи до комплексних зображень
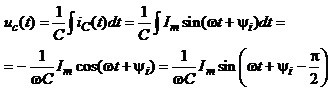 ,
,
одержуємо
. 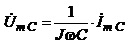 (4.24)
(4.24)
Вирази (4.22) – (4.24) показують, що для комплексних амплітуд струмів та напруг типових елементів існують алгебричні взаємозалежності, тобто так ми позбуваємось диференціальних чи інтегральних взаємозалежностей, які справедливі для миттєвих значень.
Узагальнюючи співідношення (4.22) – (4.24), їх можна подати у такому вигляді:
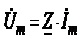 , (4.25)
, (4.25)
де Um та Im – комплексні амплітуди напруги та струму двополюсного елемента, – комплексний коефіцієнт, який називають комплексним опором цього двополюсника.
Вираз (4.25) називають законом Ома у комплексному вигляді.
Використовуючи прості тригонометричні перетворення, можна переконатись, що перехід від миттєвих значень струмів та напруг до їхніх комплексних амплітуд не порушує принципу суперпозиції і, отже, закони Кірхгофа, є справедливими і для комплексних амплітуд.
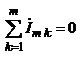 а)
а)
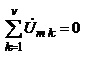 б)
. (4.26)
б)
. (4.26)
Наслідком співввідношень (4.25) та (4.26) є те, що для комплексних опорів, як і для опорів резисторів справедливі закони паралельного та послідовного з’єднання.
Комплексний опір деякого двополюсника Z як і будь-яке комплексне число, можна записати в алгебричному чи експоненціальному виглядах
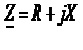 ,
,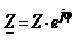
де R – активний опір двополюсника;
X – реактивний опір двополюсника;
Z – повний опір (модуль комплексного опору);
ф – аргумент комплексного опору.
Очевидно, справедливими є такі співвідношення
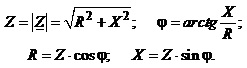
Модуль комплексного опору котушки
індуктивності 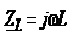 називають індуктивним опором і
позначають через XL, а модуль комплексного опору конденсатора
називають
називають індуктивним опором і
позначають через XL, а модуль комплексного опору конденсатора
називають 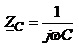 ємнісним опором та
позначають через XC
ємнісним опором та
позначають через XC
Фізичний зміст комплексного опору такий:
модуль комплексного опору (повний опір) показує, у скільки разів амплітуда напруги на елементі перевищує амплітуду струму, а аргумент є різницею початкових фаз (зсувом фаз) напруги та струму.
Поряд із поняттям комплексного опору використовується поняття комплексної провідності, яка є оберненою до опору
![]() .
.
Введені у такий спосіб комплексні амплітуди струмів та напруг і комплексні опори дають змогу розраховувати електричні кола змінного синусоїдного струму, тобто кола, які складаються з резисторів, котушок індуктивності, конденсаторів, джерел гармонічної напруги чи струму, подібно, як це було у резистивних схемах.
Відповідний метод аналізу часто називають символічним методом або методом комплексних амплітуд.
Суть названого методу така.
Крок 1. Як змінні, що характеризують електричний стан схеми, вибираємо комплексні амплітуди струмів та напруг.
Крок 2. Реальні елементи електричної схеми замінюють їхніми комплексними опорами.
Крок 3. Використовуючи той чи інший метод з п. 2.3, будують математичну модель схеми у вигляді системи комплексних рівнянь.
Крок 4. Розв’язавши отримані на кроці 3 рівняння, знаходять комплексні амплітуди шуканих струмів та напруг.
Крок 5. За знайденими на попередньому кроці комплексними амплітудами відтворюють відповідні миттєві значення струмів та напруг.
