2. . Кола змінного струму з індуктивністю та ємністю. Активна та реактивна потужність.
Кола змінного струму з індуктивністю та ємністю.
Активна та реактивна потужність.
1. Ланцюг змінного струму з індуктивністю.
2. Ланцюг змінного струму з ємністю.
3. Послідовний ланцюг змінного струму. Резонанс напруг.
4. Потужність змінного струму. Коефіцієнт потужності.
1. Ланцюг змінного струму з індуктивністю
Розглянемо ланцюг (мал. 1), у якому до котушки індуктивності L , що не
має активного опору ( R = 0), прикладена синусоїдальна напруга й по якій тече
синусоїдальний струм
![]()
Змінний струм, що протікає через котушку, створює в ній ЕРС
самоіндукції eL . Тоді у відповідності із другим правилом Кірхгофа можна
записати:

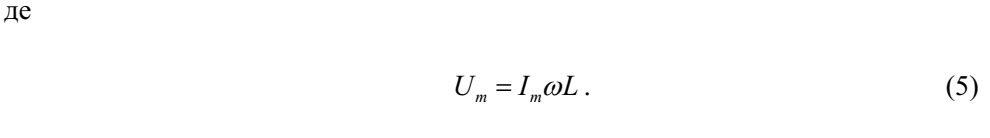
Ділячи обидві частини рівності (5) на 2 , одержимо для діючих значень
U I L = ω , звідки

З формули (6) ми бачимо, що в розглянутому ланцюзі струм відстає по
фазі від напруги на кут
π 2
. Фізично це пояснюється тим, що індуктивна
котушка реалізує інерцію електромагнітних процесів. Векторна діаграма для
цього ланцюга зображена на мал. 2, а часові – на мал. 3.
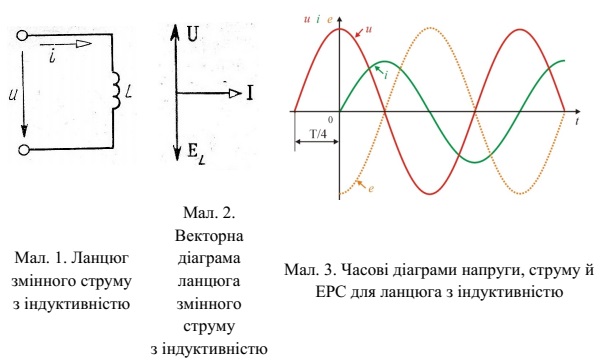 Співвідношення (6) являє собою закон Ома для ланцюга з ідеальною
Співвідношення (6) являє собою закон Ома для ланцюга з ідеальною
індуктивністю, а величина X L fL L = = ω π 2 називається індуктивним опором.
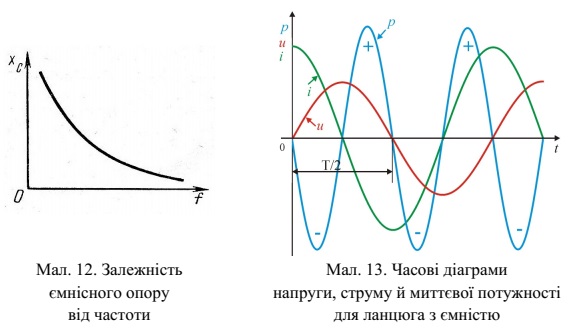
Індуктивний опір вимірюється в омах. Зі збільшенням частоти струму f
індуктивний опір X L збільшується (мал. 4). Фізично це пояснюється тим, що
зростає швидкість зміни струму, а отже, і ЕРС самоіндукції.
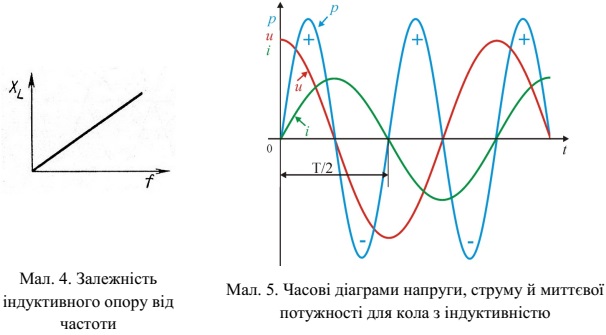
Миттєва потужність у ланцюзі із чисто індуктивним опором рівна:
![]()
Ми бачимо (мал. 5), що вона змінюється за законом синуса з подвоєною
частотою.
Позитивні значення потужності відповідають накопиченню енергії
котушкою, а негативні – поверненню запасеної енергії назад джерелу. Середня
за період потужність дорівнює нулю. Отже, ланцюг з індуктивністю потужності
не споживає, у ній відбувається лише перекачування електричної енергії від
джерела в котушку й назад. Опір такого ланцюга називають реактивним.
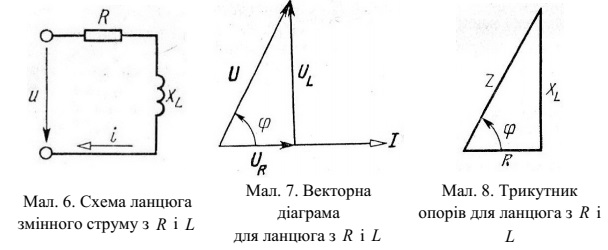
Реальні ланцюги, що містять індуктивність, завжди мають і активний
опір: опір проведення обмотки проводів. Тому розглянемо електричне коло
(мал. 6), у якім через котушку індуктивності L , що володіє активним опором R
, протікає змінний струм.
Через котушку й резистор протікає той самий струм, тому в якості
основного виберемо вектор струму й будемо будувати вектор напруги,
прикладеного до цього ланцюга.
Напруга, прикладене до ланцюга, дорівнює векторній сумі падінь напруг
на котушці індуктивності й резисторі:
U= UR+ UL (8)
Напруга на резисторі, як було показано вище, буде збігатися по фазі зі
струмом, а напруга на індуктивності буде випереджати струм на кут
π/2
Побудувавши вектори I
, і скориставшись формулою (8),
знайдемо вектор U
Векторна діаграма показана на мал. 7.
Ми бачимо, що в розглянутому ланцюзі струм I
відстає по фазі від
прикладеного напруги U
, але не на π/2, як у випадку чистої індуктивності, а на
деякий кут ϕ . Цей кут може приймати значення від 0 до π/2
й при заданій індуктивності залежить від значення активного опору: зі збільшенням R кут ϕ зменшується.
По теоремі Піфагора

. 

2. Ланцюг змінного струму з ємністю
Розглянемо електричне коло, у якім змінна напруга U t U t sin = m ω
прикладена до ємності C (мал. 9).
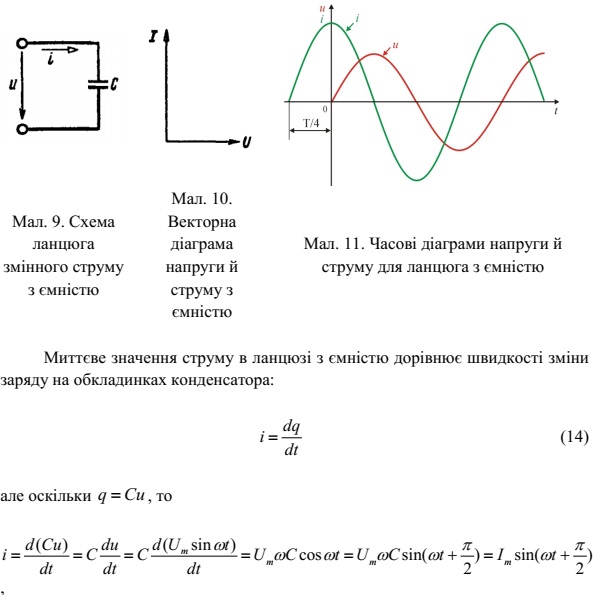

Ми бачимо (мал. 13), що миттєва потужність змінюється з подвоєною
частотою. При цьому позитивні значення потужності відповідають заряду
конденсатора, а негативні - його розряду й поверненню запасеної енергії в
джерело. Середня за період потужність тут дорівнює нулю, оскільки в ланцюзі з
конденсатором активна потужність не споживається, а відбувається обмін
електричною енергією між конденсатором і джерелом. Отже, конденсатор, так
само як і індуктивність, є реактивним опором.
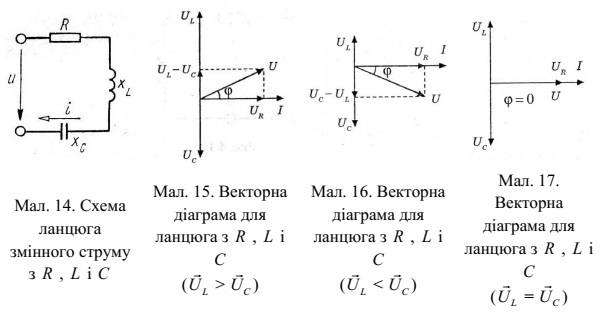
3. Послідовний ланцюг змінного струму з R, C, L. Резонанс напруг
Розглянемо тепер ланцюг змінного струму, що містить індуктивність,
ємність і резистор, включені послідовно (мал. 14).
Через усі елементи ланцюга протікає той самий струм, тому в якості
основного виберемо вектор струму й будемо будувати вектор напруги,
прикладеного до цього ланцюга. Напруга, прикладене до ланцюга, дорівнює
векторній сумі падінь напруг на котушці індуктивності, на ємності й на
резисторі:
![]()
Оскільки нам відомі амплітуди й фази цих векторів, ми можемо
побудувати векторну діаграму й знайти вектор U (мал. 15).
Із цієї векторної діаграми ми можемо знайти модуль вектора
прикладеного до ланцюга напруги Uй зрушення по фазі ϕ між струмом і
напругою:
![]()

У результаті побудови діаграми ми одержали трикутник напруг,
гіпотенуза якого дорівнює прикладеній напрузі U. При цьому різниця фаз між
струмом і напругою визначається співвідношенням векторів U L і UC. При UL>UC
(див. мал. 15) кут ϕ позитивний і навантаження має індуктивний характер,
при UL<UC кут ϕ негативний і навантаження має ємнісний характер (мал. 16),
а при UL=UC кут ϕ дорівнює нулю й навантаження є чисто активним (мал.17).
Трикутнику напруг відповідає трикутник опорів. Наприклад, для кола з
активним і індуктивним опорами ( X X L C > або X C = 0, мал. 18) і кола з
активним і ємнісним опором ( X X C L > або X L = 0, мал. 19).


При резонансі напруг частота джерела дорівнює власній частоті коливань
контуру.
Вираження (24) є формулою Томсона, що визначає залежність власної
частоти коливань контуру f0 від параметрів L і C .
4. Потужність змінного струму. Коефіцієнт потужності.
Інтенсивність процесів одержання, передачі, перетворення й споживання
електричної енергії визначає потужність. Залежно від характеру процесів, що
відбуваються в ланцюгах змінного струму, розрізняють активну, реактивну та
повну потужність.
Активна потужність P характеризує величину споживаним ланцюгом
енергії, що не вертається джерелу живлення, тобто енергії, що переходить
безповоротно з електричної в інші види – наприклад, теплоту або механічну
роботу.
Реактивна потужність визначає інтенсивність обміну електричною
енергією між джерелом і реактивним навантаженням.
Повна потужність визначає вимоги, пропоновані до джерела живлення,
його габарити й вартість. Джерело повинно бути розраховане на споживані
ланцюгом струм і напругу, незалежно від величини активної потужності. Ця
величина вказується на табличках приладів змінного струму.
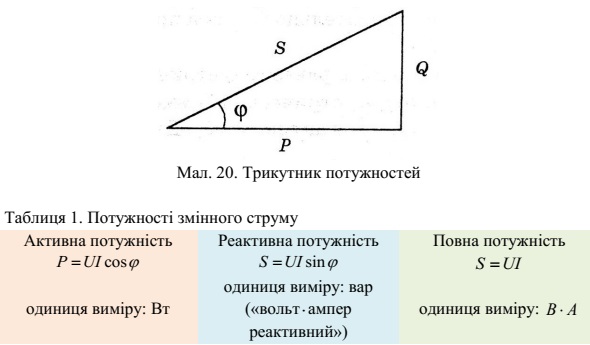
Повна потужність і її складові зв'язані між собою співвідношенням
![]()
і можуть бути представлені трикутником потужностей, який подібний до
трикутників напруг і опорів (мал. 20).
Активна (корисна) потужність P залежить від струму, напруги й cosϕ .
При збільшенні кута ϕ зменшуються cosϕ й потужність P , а при зменшенні
кута ϕ активна потужність P зростає. Таким чином, cosϕ показує, яка частина
повної потужності теоретично може бути перетворена в інші види енергії.
Величина cosϕ називається коефіцієнтом потужності.
Для більш раціонального використання потужності змінного струму,
вироблюваного джерелами електричної енергії, потрібно намагатися зробити
навантаження таким, щоб cosϕ ланцюгу був близький до одиниці. На практиці
в масштабах підприємства добитися цього досить важко, і гарним показником є
cosϕ , рівний 0,9-0,95.
