Тема 1. Електричні кола постійного струму
Тема 2. Електричні кола постійного струму
1. Електричний струм. Сила струму.
2. Електрорушійна сила і її джерела.
3. Електричний опір. Резистор. Закон Ома для ділянки
кола.
4. Електричне коло і його елементи. Закон Ома для замкненого кола.
5. Режими роботи джерел ЕРС.
6. Робота й потужність струму.
7. Теплова дія струму.
8. Схеми електричних кіл.
9. Закони Кірхгофа. З'єднання резисторів.
10. Робота джерела в режимі генератора й споживача.
11. Застосування законів Кірхгофа для розрахунку електричних кіл.
11. . Застосування законів Кірхгофа для розрахунків електричних кіл
11. Застосування законів Кірхгофа для
розрахунків електричних кіл
Складним називають розгалужене електричне коло, що
містить довільне
число джерел і споживачів, яку неможливо звести до
комбінації послідовних і паралельних
з'єднань.
Для розрахунків складного ланцюга застосовують закони
Кірхгофа, при
цьому необхідно скласти стільки незалежних рівнянь,
скільки гілок у схемі (m).
Спочатку складають рівняння за першим законом Кірхгофа.
Для цього
довільно задаються напрямками струмів і позначають їх
стрілками. При цьому якщо схема має n вузлів, те можна скласти тільки (n-1) незалежних
рівнянь, тому що рівняння для останнього вузла буде наслідком попередніх. Тому
длякожного вузла, крім останнього, записуємо рівняння: у лівій частині - алгебраїчна
сума струмів (струми, спрямовані до вузла, тобто "втікають" у
вузол, беруться зі знаком "плюс", а струми, які
спрямовані від вузла, тобто
"витікають" з нього - зі знаком
"мінус"), у правій частині - нуль.
Інші рівняння складають за другим законом Кірхгофа. Тут
теж треба
пам'ятати, що незалежні рівняння можна скласти тільки для
тих контурів, які не утворюються в результаті накладення вже розглянутих, тобто
кожний новий контур повинен містити принаймні одну нову гілку, яка не входила в
рівняння, уже складені для інших контурів. Вибирають напрямок обходу контуру,
як правило, за годинниковою стрілкою. Після чого складають рівняння, де в лівій
частині - алгебраїчна сума напруг на всіх опорах контуру, а в правій частині - алгебраїчна
сума ЕРС. При цьому позитивними (зі знаком "плюс") уважають ті струми
й ЕРС, напрямку яких збігаються з напрямком обходу контуру, а негативними, (зі
знаком "мінус") - напрямки яких протилежні напрямку обходу.
Розв'язок отриманої системи лінійних алгебраїчних рівнянь
дає значення
струмів у галузях схеми.
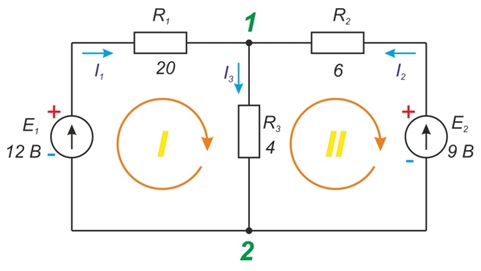
Мал. 5. Схема складного ланцюга
Так, у схемі на мал. 5 три гілки (m=3, тому що
необхідно знайти три
струми й скласти для цього три рівняння), два вузли (n=2), два
незалежні
контури.
Для вузла 1 рівняння, складене по першому закону
Кірхгофа, буде мати
вигляд:
Для
вузла 2 рівняння складати нема рації.2 рівняння, що залишилися, складаємо за
другим законом Кірхгофа.
Виберемо два незалежні контури (на малюнку 5 позначені
римськими
цифрами I, II) і
приймемо їхній обхід за годинниковою стрілкою. Тоді за
другим законом Кірхгофа
одержимо:
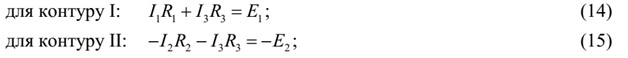
Рівняння (13), (14), (15) становлять систему незалежних
лінійних
алгебраїчних рівнянь, розв'язок якої дає значення струмів
у галузях схеми:
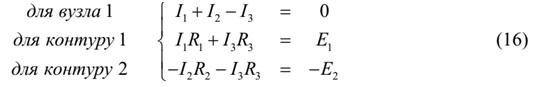
Скористаємося методом Гауса. Із третього рівняння
виразимо I3, із
другого I2 й
підставимо їх у перше рівняння.
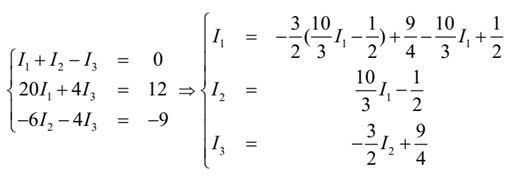
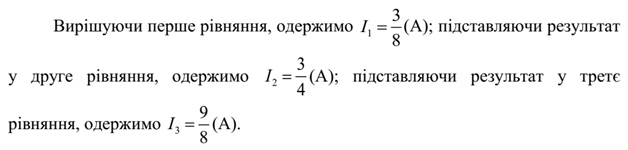
При відсутності сучасних засобів обчислювальної техніки
розв'язок
системи з великим числом рівнянь методом Гауса, по
формулах Крамера й т.п. методами лінійної алгебри був досить трудомістким. У
цьому випадку було зручніше скористатися іншими методами розрахунків ланцюгів,
так само заснованими на законах Кірхгофа, але таких, що дозволяють зменшити
число рівнянь у системі – методами контурних струмів, вузлових напруг і ін.