3. Зображення змінного струму методом векторних діаграм

Метод векторних діаграм, тобто зображення величин, що
характеризують змінний струм векторами, а не тригонометричними функціями, надзвичайно зручний. Тому коротко викладемо його основи.
Змінний струм на відміну від постійного характеризується двома
скалярними величинами - амплітудою й фазою. Тому для математичного опису змінного струму необхідний математичний об'єкт, що також характеризується двома скалярними величинами. Існують два такі математичні об'єкти (з відомих нам) - вектор на площині й комплексне число. У теорії електричних кіл і ті й інші використовуються для опису змінних струмів.
При описі електричного ланцюга змінного струму за допомогою векторних діаграм кожному струму й напрузі зіставляється вектор на площині в
полярних координатах, довжина якого дорівнює амплітуді струму або
напруги, а полярний кут - відповідний до фази.
Нехай заданий синусоїдальний струм
i =  I m sin(ωt+ ψ) .
Графік цього струму має вигляд синусоїди, зображеної на мал. 4. Поруч
зображений вектор, що відповідає побудованій синусоїді. Цей вектор із
модулем, що дорівнює амплітуді, нахилений до горизонтальної осі під кутом ψ.


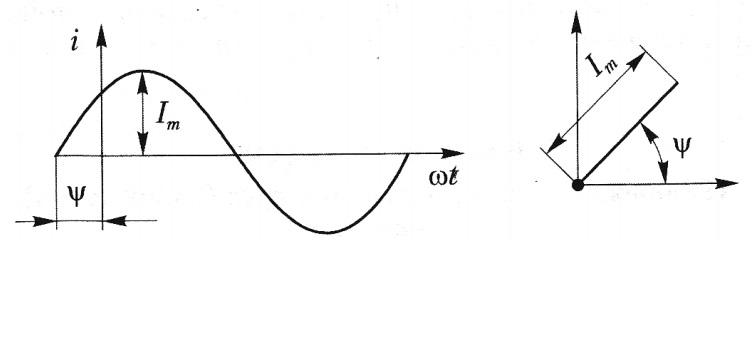
Мал. 4. Графік синусоїдального струму і його векторна діаграма
Оскільки фаза змінного струму залежить від часу, уважається, що всі
вектори обертаються проти годинникової стрілки із частотою змінного струму.
Векторна діаграма будується для фіксованого моменту часу.
Більш докладна побудова й використання векторних діаграм буде викладена нижче на прикладах конкретних ланцюгів.