Похожие презентации:
Ейлерові графи. Гамільтонові графи
1. Лекція 9. Ейлерові графи. Гамільтонові графи
2. §1 Ейлерові графи
Однією з перших задач теорії графів упрацях видатного математика ХVIII сторіччя Л.
Ейлера була задача щодо кенігсберзьких мостів.
Якщо існує цикл у графі, в якому кожне
ребро графа брало участь один раз, то такий
цикл називається ейлеровим циклом, а граф,
який містить такий цикл, – ейлеровим графом.
3.
Скінченний граф G є ейлеровим графом тоді йлише тоді, коли:
1) G – зв’язний;
2) усі його вершини мають
парні степені.
Графи, що не мають ейлерового циклу, але
мають
ейлеровий
ланцюг
називають
напівейлеровими. Такі графи мають дві вершини
непарного степеню, ланцюг починається в одній
з них, а закінчується в іншій.
8
4
9
7
1
5
10 6
3
2
4. §2 Гамільтонові графи
Гамільтоновимциклом
називається
простий цикл, що проходить через усі вершини
розглянутого графа.
Гамільтонів
цикл
названо
іменем
ірландського математика Вільямса Гамільтона,
який 1859 року вперше почав вивчати ці питання.
Він розглядав задачу мандрівника: обійти всі
столиці заданих країн (вершини графа) по одному
разу і повернутися в першу.
ЗАУВАЖЕННЯ. Гамільтонів цикл існує
далеко не в кожному графі. Через кожні дві
вершини графа може проходити простий цикл, а
гамільтонів цикл при цьому може бути відсутній.
5.
Для 20 країн задача є обходом додекаедра:1-2-3-4-5-6-7-8-9-10-11-12-13-14-15-16-17-18-19-20-1
6.
Гамільтонові графи7.
Графи, які не мають гамільтонових циклівГраф, який має гамільтонів
ланцюг
називають
напівгамільтоновим.
8. Дерева.
9. §1 Основні визначення
Деревом називається зв’язний граф безциклів.
Дерево не може мати ані кратних ребер, ані
петель, ані ізольованих вершин.
Кожний ланцюг у дереві є простий, через те
що в іншому разі дерево містило б цикл, що є
неможливе.
При додаванні до дерева ребра утворюється
цикл, а при вилученні хоча б одного ребра дерево
розпадається на компоненти, кожна з яких є або
деревом,або ізольованою вершиною.
Дерева називаються істотно різними,
якщо вони не є ізоморфні.
10.
Усі можливі дерева з шістьма вершинами –неізоморфні.
11.
Теорема (перелічуються властивості дерев,кожна з яких повністю схарактеризовує дерево).
Еквівалентні є такі означення дерева:
а) дерево – це зв’язний граф без циклів;
б) дерево – це зв’язний граф, у якому кожне ребро
є перешийком;
в) дерево – це зв’язний граф, цикломатичне число
якого дорівнює нулеві;
m – n + 1 = 0 або m = n – 1, тобто у кожному дереві
кількість ребер є на одиницю менша за кількість
вершин.
г) дерево – це граф, у якому для кожних двох
вершин існує лише один з’єднувальний ланцюг.
12. §2 Остовне (Кістякове) дерево графа
§2 Остовнеграфа
(Кістякове)
дерево
Вилучання з довільного зв’язного графа
всіх циклових ребер дає в наслідок дерево
T = ( X′, U′) таке, що:
1) X′ = X, тобто множина вершин дерева T
збігається з множиною вершин графа G;
2) U′ ⊆ U, тобто кожне ребро дерева є водночас
ребром графа G.
Кожне дерево T, яке задовольняє умовам 1)
та 2) називається кістяковим деревом графа G.
ЗАУВАЖЕННЯ. Через те, що вилучання циклових
ребер можна провадити у різні способи, то один і
той самий граф має багато кістякових дерев.
13.
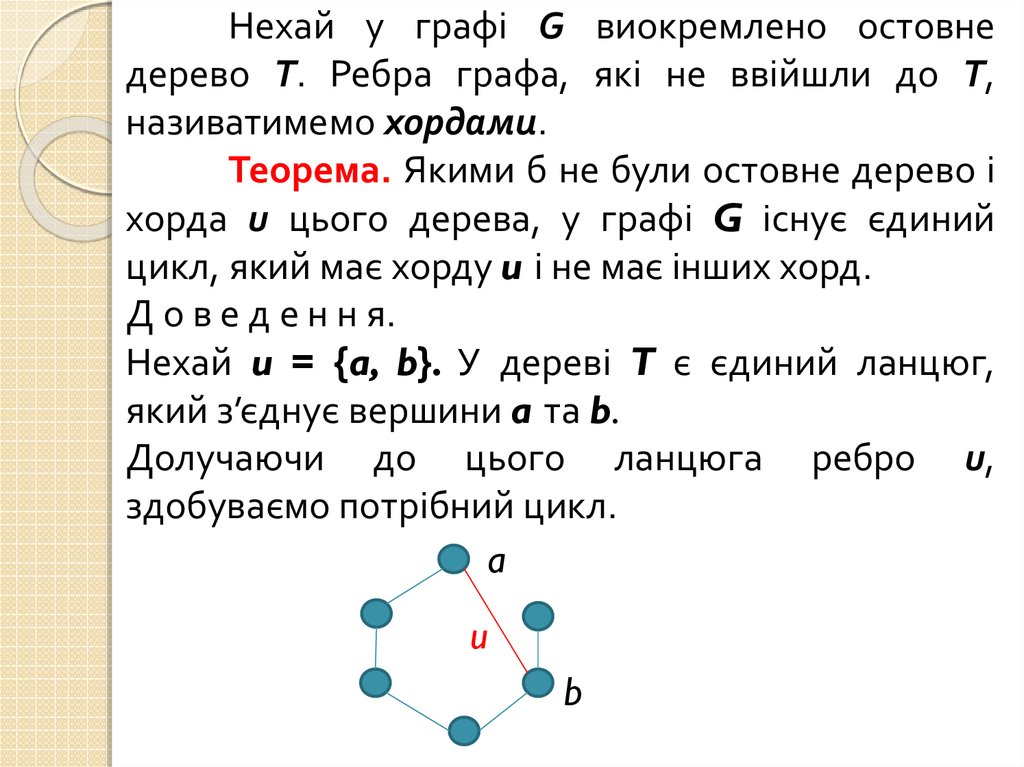
Нехай у графі G виокремлено остовнедерево T. Ребра графа, які не ввійшли до T,
називатимемо хордами.
Теорема. Якими б не були остовне дерево і
хорда u цього дерева, у графі G існує єдиний
цикл, який має хорду u і не має інших хорд.
Д о в е д е н н я.
Нехай u = {a, b}. У дереві T є єдиний ланцюг,
який з’єднує вершини a та b.
Долучаючи до цього ланцюга ребро u,
здобуваємо потрібний цикл.
a
u
b
14.
Граф GОстовні дерева Т
Т1
Т3
Т4
Т2
Т5
15.
Довільний незв’язний граф, який немістить циклів, називається лісом.
Еквівалентне визначення лісу: граф G, усі
компоненти зв’язності якого є деревами,
називається лісом.
Граф G
16. §3 Кореневі дерева
Дерево – це сукупність елементів, щоназиваються вузлами (один з яких корінь), та
відношень („батьківських”), що утворюють
ієрархічну структуру вузлів. Вузли можуть
бути елементами будь-якого типу (літерами,
рядками, числами).
Піддерево, корінь якого знаходиться в лівому
(правому) нащадку вершини, називається лівим
(правим) піддеревом цієї вершини.
17.
Висота вузла дерева - це довжина самогодовгого шляху з цього вузла до будь-якого
листа.
Висота дерева співпадає з висотою кореня.
Глибина вузла – це довжина шляху від кореня
до цього вузла.
Степінь вузла – це кількість дуг, що з нього
виходить.
Степінь дерева дорівнює максимальному
степеню вузла, що входить у дерево.
Листя в дереві - це вузли, що мають степінь
нуль.
Бінарне дерево – це дерево степінь якого
дорівнює два .
Дерева,
степінь
яких
більше
двох,
називаються розгалуженими.
18.
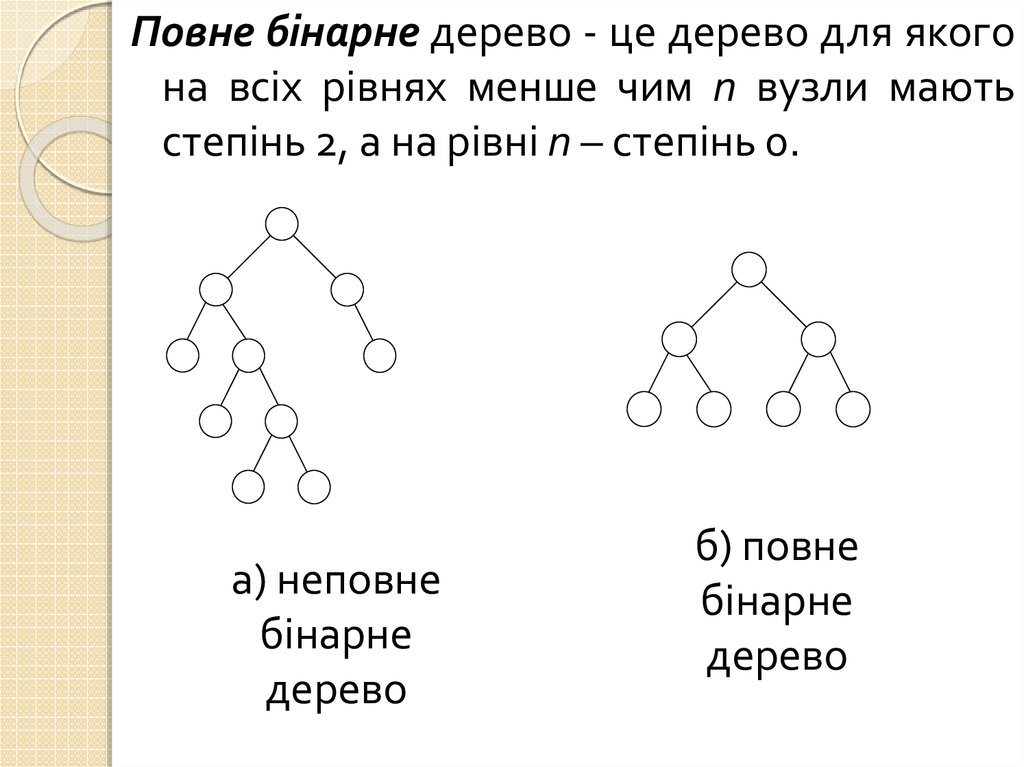
Повне бінарне дерево - це дерево для якогона всіх рівнях менше чим n вузли мають
степінь 2, а на рівні n – степінь 0.
а) неповне
бінарне
дерево
б) повне
бінарне
дерево
19.
Строго бінарне дерево складається тільки звузлів, що мають степінь 2 або 0.
Нестрого бінарне дерево містить вузли зі
степенем 1.
а) строго
бінарне дерево
б) нестрого
бінарне дерево
20. §4 Застосування графів і дерев
4.1 У вигляді графа можуть бути зображені:1) Електричні і транспортні мережі;
2) Карти автомобільних, залізничних та
повітряних шляхів;
21.
3) Структури молекул хімічних речовин;4) Моделі кристалів;
5) Моделі ігор;
6) Інформаційні і комп'ютерні мережі;
7) Ієрархічна структура книг;
22.
8) План діяльності або план виконання певнихробіт
(розклад).
Наприклад,
можливість
переливання крові:
9) Лабіринти;
10) Різні математичні об'єкти (відношення,
алгоритми, програми тощо)
23.
11) Генеалогічні дерева.24.
4.2 Задачі, які розв'язують за допомогою графів:1) Доставка (товари, послуги) – необхідно
визначити маршрути мінімальної довжини,
мінімальної вартості тощо.
2) Інспектування
розподілених
систем
(електромереж, телефонних, залізничних ліній).
3) Теорія ігор, головоломки.
4) Комунальне господарство, планування.
5) Складання розкладу.
6) Проектування комп'ютерних мереж.






















 Математика
Математика








