Тема 15. Векторне керування асинхронними двигунами
| Сайт: | Освітній сайт КНУБА |
| Курс: | Автоматизація електромеханічних систем в будіндустрії(Ковал) |
| Книга: | Тема 15. Векторне керування асинхронними двигунами |
| Надрукував: | Гість-користувач |
| Дата: | понеділок, 23 лютого 2026, 06:55 |
Опис
Тема 15. Векторне керування асинхронними двигунами
1. Розвиток асинхронного електроприводу з векторним керуванням
2. Векторна модель асинхронного двигуна
2.1. Поняття узагальненого вектора
2.2. Основні співвідношення між струмами і потокозчеплення АД
2.3. Індуктивність складової нульової послідовності
2.4. Рівняння статора і ротора в векторній формі
1. Розвиток асинхронного електроприводу з векторним керуванням
1. Розвиток асинхронного електроприводу з векторним керуванням.
Сучасні системи векторного керування пройшли довгий шлях розвитку і в даний час є найбільш поширеними серед систем електроприводу змінного струму. Вони дозволяють просто і ефективно управляти такими складними об'єктами як асинхронний двигун з короткозамкненим ротором (АД), що в свою чергу, дозволяє істотно розширити область його застосування, майже повністю витісняючи з автоматизованих керованих приводів двигуни постійного струму. Це пов'язано в першу чергу з розвитком силової електроніки, що дозволяє створювати надійні і відносно дешеві перетворювачі, а також з розвитком швидкодіючої мікроелектроніки, здатної реалізувати алгоритми управління практично будь-якої складності. Тому високоякісний асинхронний векторний електропривод (АВП) в даний час є по суті технічним стандартом.
Першим етапом процесу розвитку АВП була розробка універсальної векторно-матричної математичної моделі, що отримала назву узагальненої електричної машини, яка почалася в кінці 20-х років і завершилася в кінці 40-х років ХХ століття. Ця модель дозволяє описувати електромагнітні процеси в ідеалізованій електричній машині за допомогою апарату лінійної алгебри. Практичне використання моделі було відкладено на кілька десятиліть, тому що при ручних розрахунках вона не давала жодних переваг, але вимагала істотних обчислювальних витрат, теоретично ж її успішно використовували для аналізу перехідних процесів в електричних машинах.
У 1971 році F. Blaschke запропонував принцип побудови системи управління асинхронним двигуном, в якому використовувалася векторна модель АД з орієнтацією системи координат по потокозчепленню ротора. Сутність запропонованого методу, який отримав згодом назву векторного, полягала у використанні в системі управління передавальних функцій зворотних по відношенню до передавальних функцій векторної моделі АД, що дозволяло отримати в якості незалежних вхідних змінних системи величини, що входять в рівняння електромагнітного моменту. Тому цей принцип називається також прямим управлінням моментом. Крім того, для спрощення завдання в векторної моделі АД використовувалася система координат, орієнтована по одному з векторів, що входять в рівняння електромагнітного моменту, що істотно спрощувало передавальні функції системи і дозволяло визначити момент двома незалежними змінними аналогічно тому, як це робиться в двигунах постійного струму.
За три минулі десятиліття були розроблені десятки варіантів вихідних моделей АВП, реалізовані сотні пристроїв на різній елементній базі, опубліковані тисячі статей і монографій, але принцип і перша модель, запропонована F. Blaschke, як і раніше домінують в технічних реалізаціях.
2. ВЕКТОРНА МОДЕЛЬ АСИНХРОННОГО ДВИГУНА
Більшість електричних машин змінного струму призначений для роботи в трифазних мережах, тому вони будуються з симетричними трифазними обмотками на статорі, причому МДС цих обмоток розподілені в просторі за законом близьким до синусоидальному, тобто МДС, створювана k-й обмоткою в точці, віддаленій від осі цієї обмотці на кут a k дорівнює -Fa k = Fk0cosa k, де Fk0 - МДС, відповідна осі k-й обмотки. Синусоидальность розподілу дозволяє уявити МДС або пропорційні їм струми узагальненим просторовим вектором на комплексній площині, тобто вектором, що представляє собою геометричну суму відрізків, побудованих на просторових осях фазних обмоток і відповідних миттєвим значенням фазних МДС або струмів. При цьому проекції узагальненого вектора на осі фазних обмоток в будь-який момент часу будуть відповідати миттєвим значенням відповідних величин.
2.1. Поняття узагальненого вектора
2.1. Поняття узагальненого вектора.
Більшість електричних машин змінного струму призначений для роботи в трифазних мережах, тому вони будуються з симетричними трифазними обмотками на статорі, причому МДС цих обмоток розподілені в просторі за законом близьким до синусоидальному, тобто МДС, створювана k-й обмоткою в точці, віддаленій від осі цієї обмотці на кут a k дорівнює -Fa k = Fk0cosa k, де Fk0 - МДС, відповідна осі k-й обмотки. Синусоидальность розподілу дозволяє уявити МДС або пропорційні їм струми узагальненим просторовим вектором на комплексній площині, тобто вектором, що представляє собою геометричну суму відрізків, побудованих на просторових осях фазних обмоток і відповідних миттєвим значенням фазних МДС або струмів. При цьому проекції узагальненого вектора на осі фазних обмоток в будь-який момент часу будуть відповідати миттєвим значенням відповідних величин.
При симетричній трифазній системі обмоток узагальнений вектор струму можна представити у вигляді
(1.1.1)
Де
оператори повороту, а ia, ib і ic - миттєві значення струмів відповідних обмоток. Позначення вектора рядковим символом прийнято для вказівки на те, що його координати є функціями часу аналогічно тому, як рядкові символи при позначенні скалярних величин вказують на миттєве значення.
При такому поданні фазні струми ia, ib і ic можна розглядати як проекції вектора i на відповідні осі фазних обмоток (рис. 1.1 а)). Якщо провести побудова вектора i, відкладаючи значення фазних струмів ia, ib і ic на осях обмоток (рис. 1.1 б)), то сумарний вектор виявиться в півтора рази більше того вектора, проекції якого відповідають фазним струмів. Тому в вираженні (1.1.1) присутній коефіцієнт 2/3, що призводить модуль сумарного вектора до такого значення, яке при проектуванні на осі фазних обмоток дасть істинні значення фазних струмів.
Якщо статор машини має нульовий провід, то фазні струми можуть містити
нульову складову і їх значення можна представити у вигляді ia + io, ib + io і
ic + io. Тоді вектор струму дорівнює
Таким чином, узагальнений вектор струму статора не містить нульовий складової і її при аналізі слід враховувати особливо.
Узагальнений вектор, як і будь-який вектор на комплексній площині, можна уявити алгебраїчної формою записи комплексного числа. Зазвичай це роблять, поєднуючи речову вісь з віссю обмотки a (рис. 1.1), тоді
Підставляючи у вираз (1.1.1) значення операторів повороту, записані в алгебраїчній формі, і розділяючи речову і уявну частини отримаємо
Якщо фазні струми містять нульову складову, то її значення буде рівним . Перехід від уявлення узагальненого вектора через проекції на осі трифазних
обмоток до подання через проекції на осі комплексної площини еквівалентно
перетворенню трифазної системи обмоток в еквівалентну двухфазную. У матричної
формі це перетворення можна записати у вигляді
(1.1.2)
Звідси зворотне перетворення координат узагальненого вектора –
(1.1.3)
Узагальнений вектор можна представити також у обертається системі координат. Якщо вектор струму представлений в нерухомій системі координат a -b, то перехід до нової системи координат xy, розгорнутої щодо вихідної на деякий кут J (xy) (рис. 1.2 а)), здійснюється з очевидного співвідношення аргументів комплексних чисел у вигляді
(1.1.4)
При цьому слід зауважити, що на кут (xy) не накладалися ніяких обмежень, тобто він може мати постійне значення, але може також змінюватися довільним чином. Для системи координат обертається з постійною кутовою частотою w (xy) він дорівнює - J (xy) = w (xy) t.
Перетворення координат можна записати в розгорнутому вигляді наступним чином
.
Звідси можна знайти складові вектора ix і iy в матричній формі
(1.1.5)
а також зворотне перетворення
(1.1.6)
Перетворення координат можна здійснити не тільки від нерухомої системи до обертової, але і для двох систем координат, що обертаються з різними кутовими частотами. Нехай вектор i представлений в системі координат dq, поточний кут якої щодо нерухомих координат становить (dq) (рис. 1.2 б). Тоді з очевидних співвідношень кутів перетворення координат можна записати у вигляді
(1.1.7)
Узагальненими векторами можна уявити також напруги u і потокозчеплення y, при цьому всі властивості розглянутого вище узагальненого вектора струму будуть властиві й цим векторам.
2.2. Основні співвідношення між струмами і потокозчеплення АД
2.2. Основні співвідношення між струмами і потокозчеплення АД.
Якщо знехтувати насиченням муздрамтеатру АТ, то магнітні потоки, зчіплюються з його обмотками, будуть пропорційні відповідним МДС. Розглянемо основні співвідношення між цими величинами.
Припустимо, що статор і ротор трифазного АД симетричні, параметри обмотки ротора приведені до обмотці статора і робочий зазор машини рівномірний. Схематично ці обмотки показані на рис. 1.3.
З обмоткою фази a статора зчіплюються магнітні потоки, створювані як нею самою, так і всіма іншими обмотками. Частина магнітного потоку, створюваного самої обмоткою зчіплюється тільки з її власними витками і називається потоком розсіювання. Інша частина, крім витоків самої обмотки охоплює також витки інших обмоток і називається головним або основним магнітним потоком. Індуктивність L1, що зв'язує потік розсіювання обмотки з протікає в ній струмом, називається індуктивністю розсіювання, а індуктивність lm, яка визначає потокозчеплення з основним потоком - взаємною індуктивністю або індуктивністю основного потоку. Користуючись цими величинами, можна уявити потокозчеплення фази a при відсутності струмів в обмотках ротора у вигляді
(1.2.1)
де Mab і Mac - взаємні індуктивності статорних обмоток.
Якщо дві обмотки статора АД мають однакові параметри, то магнітний потік, створюваний струмом другий обмоткою і зчіплюються з витками першої, буде повністю ідентичний потоку, створюваному першої обмоткою і зчіплюються з витками другий, за умови однакових струмів і збіги розташування осей двох обмоток в просторі. Очевидно, що за цих умов картина магнітного поля буде однаковою незалежно від того, з якої з обмоток протікає струм. Отже, індуктивність основного потоку статорних обмоток буде дорівнює їх взаємної індуктивності за умови поєднання геометричних осей.
Зсув осей обмоток в просторі на кут q викличе зміна їх взаємної індуктивності, пропорційне косинусу кута зрушення, тобто M = M0cosq = lmcosq, де M0 = lm - взаємна індуктивність обмоток при поєднанні їх осей. При відсутності нульового проводу ia + ib + ic = 0 Þ ib + ic = - ia і вираз (1.2.1) можна перетворити з урахуванням того, що q b = 120° і q c = - 120° до виду
(1.2.2)
Індуктивність L1 відповідає повною індуктивності обмотки статора, що включає її індуктивність від потоку розсіювання L1s, індуктивність від частини основного магнітного потоку, створеної самою обмоткою lm, і індуктивність від частини основного потоку, створеної двома іншими обмотками статора lm / 2. Таким чином, повна індуктивність обмотки статора від основного магнітного потоку Lm в 3/2 рази більше її індуктивності lm, розрахованої при відсутності струмів в інших обмотках.
В силу симетрії статора, для інших обмоток можна записати аналогічні вирази
-, а потім, аналогічно виразу (1.1.1), об'єднати фазні проекції в
узагальнений вектор потокозчеплення статора при відсутності струмів ротора –
(1.2.3)
Слід зауважити, що при аналізі индуктивностей не вводилося ніяких обмежень на просторовий розподіл магнітного потоку по зазору машини, тому отримані вирази справедливі при будь-якому характері розподілу поля.
Наявність струмів в обмотках ротора призведе до появи додаткових складових потокозчеплення обмоток статора. Якщо вісь фази a ротора зміщена в просторі на деякий кут a (рис. 1.3), то взаємні індуктивності обмоток ротора і фази a статора можна визначити через відповідні кути, утворені їх осями в вигляді –
де M0a, M0b і M0c - взаємні індуктивності при = 0. Тоді повне потокозчеплення обмотки фази a статора при наявності струмів ротора і з урахуванням того, що нульовий провід ротора відсутня, буде
(1.2.4)
Але взаємна індуктивність обмоток фази a статора і ротора при нульовому зміщенні осей M0a дорівнює lm, тому що параметри обмоток ротора приведені до статорних і наближено можна вважати, що при збігу їх осей картина магнітного поля буде такою ж, як при збігу осей статорних обмоток. Тому
(1.2.5а)
і за аналогією для двох інших фаз:
(1.2.5б)
Об'єднуючи потокосцепления фазних обмоток в узагальнений вектор потокозчеплення, отримаємо
(1.2.6)
Аналогічне вираз, в силу симетрії зв'язків між статором і ротором, можна записати для потокозчеплення ротора –
(1.2.7)
У виразах (1.2.6) і (1.2.7) вектори струму ротора і статора записані в різних системах координат. Так в першому вираженні ток статора записаний в нерухомій системі координат a -b, пов'язаної зі статором, а струм ротора під обертається (зміщений на поточний кут a) системі координат x-y, пов'язаної з ротором, тобто в повній записи з індексами систем координат –
або, якщо обидві частини виразу (1.2.6) помножити на оператор повороту e- ja
Таким чином, під час запису узагальнених векторів в однакових системах координат вираження для потокосцепления мають однакову форму і індекси системи в них можна опустити. Тоді остаточно потокосцепления статора і ротора з урахуванням всіх струмів АД і незалежно від обраної системи координат можна представити у вигляді
(1.2.8а)
(1.2.8б)
З виразів (1.2.8) випливає, що потокосцепления статора і ротора розкладаються на складові обумовлені власним струмом (y 11 і y 22) і струмом іншій частині АТ (y 12 і y 21).
Користуючись тим, що сума струмів статора і ротора утворює струм
намагнічування АД, тобто , Потокозчеплення статора і
ротора можна також представити через основний магнітний потік
і потоки розсіювання статора
і ротора
-
(1.2.9а)
(1.2.9б)
2.3. Індуктивність складової нульової послідовності
2.3. Індуктивність складової нульової послідовності.
Різного виду асиметрія параметрів АД і / або джерела живлення викликає при наявності нульового проводу появи струмів нульової послідовності в обмотках статора. Так як для нульової складової справедливо ia0 = ib0 = ic0 = i0, то, підставляючи ці значення у вираз (1.2.2) для потокосцепления обмотки фази a статора, отримаємо
.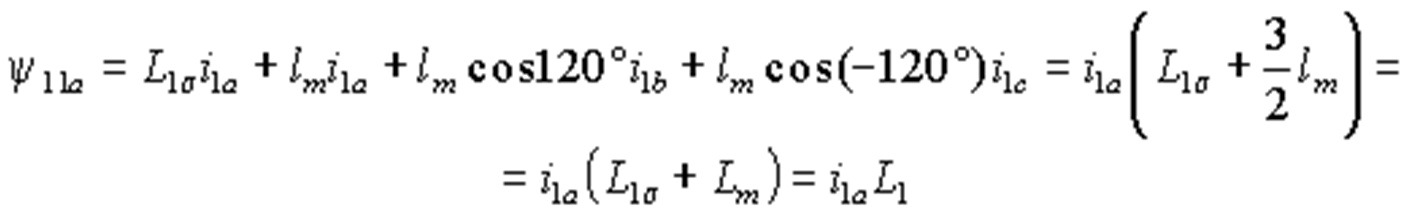
Очевидно, що аналогічні викладки для потокозчеплення обмоток фаз b і c приведуть до такого ж результату, тобто y 1a0 = y 1b0 = y 1c0 = L1s i0. Таким чином, потокосцепления складових нульової послідовності для всіх обмоток однакові і визначаються індуктивністю розсіювання L1s.
2.4. Рівняння статора і ротора в векторній формі
2.4. Рівняння статора і ротора в векторній формі.
Рівняння Кірхгофа для фазних напруг статора АД мають вигляд
(1.4.1)
При наявності нульових складових до виразів (1.4.1) слід додати рівняння
Перейдемо до векторної формі записи виразів (1.4.1), помноживши друге рівняння на A, а третє на A2, а потім складаючи всі три рівняння і примножуючи їх праву і ліву частини на 2/3. В результаті отримаємо
(1.4.2)
Аналогічні перетворення можна виконати з системі координат x-y і для фаз ротора, отримавши при цьому
(1.4.3)
Рівняння (1.4.2) і (1.4.3) записані в різних системах координат. Для
перекладу рівняння ротора в нерухому систему координат a -b
помножимо обидві його частини на оператор повороту на поточний кут повороту
системи координат θ - ejθ і представимо в похідній вектор потокозчеплення
ротора в новій системі як . Після
перетворень, опускаючи індекси координатної системи, отримаємо рівняння ротора
в векторній формі в системі координат статора
(1.4.4)
де w = dθ / dt - поточна швидкість обертання ротора.
Перехід до нерухомої системі координат в рівнянні ротора привів до розкладання доданка, відповідного ЕРС індукції, на дві складові: перша складова dy 2 / dt пов'язана зі зміною потокосцепления в часі внаслідок вимірювання в часі струмів і називається ЕРС трансформації, за аналогією з процесами її порушення у відповідній електричної машині; друга - w y 2 пов'язана зі зміною потокосцепления внаслідок обертання ротора і називається ЕРС обертання. Розкладання ЕРС індукції на складові є математичною операцією, пов'язаної з перетворенням системи координат за умови інваріантності потужності і в деяких випадках це розкладання можна витлумачити, виходячи з фізичних процесів в машині.
Рівняння (1.4.2) і (1.4.4) записані для нерухомої системи координат і їх можна об'єднати в загальну систему для вирішення. Крім того, обидва цих рівняння можна представити в деякій довільній системі координат mn, що обертається з довільною кутовою частотою w (mn). Для цього з ними потрібно виконати перетворення аналогічні виразами (1.4.4), в результаті яких ми отримаємо рівняння:
(1.4.5)
з яких рівняння для будь-яких інших систем координат виходять підстановкою в (1.4.5) відповідної частоти обертання w (mn).
Вирази (1.4.5) показують, що вибором системи координат можна спростити завдання, виключивши ЕРС обертання, але тільки в одному з рівнянь.
Надалі ми будемо використовувати такі індекси систем координат:
У будь-якої електричної машині кутова частота обертання магнітного поля
статора Ω1 пов'язана з кутовою частотою обертання
магнітного поля ротора Ω2 і
кутовою частотою обертання ротора Ω наступним співвідношенням -, де позитивний знак відповідає однаковому напрямку обертання. Але частоти
обертання полів статора і ротора визначаються частотами відповідних струмів і числом пар полюсів
обмоток zp, тобто
і
, де w 1 і w 2 - частоти струмів статора і ротора. Звідси
(1.4.6)
де - кутова частота обертання ротора електричної машини з однією парою
полюсів.