Тема 8_2. Інтегральні мікросхеми, основні параметри. Логічні елементи і цифрові пристрої.

3. Логічні елементи

В основі цифрової електроніки лежить двійкова система числення. Для

запису чисел у двійковій системі потрібні тільки дві цифри - нуль (0) і одиниця (1). Двійкова система числення використовується в цифрових ланцюгах завдяки тому, що двійкові цифри легко представити у вигляді двох напруг - високої й низької.
У логічних ланцюгах можливі два стани - 1 і 0. Стан 1 також називають
високим, щоб указати, що напруга в цьому стані вище, чим у стані 0. Стан 0
також називають низьким, щоб указати, що напруга в цьому стані нижче, ніж у стані 1.
Дані у двійковій системі представляються двійковими цифрами, які
називаються бітами. Біт - двійкова цифра (розряд) (binary digit).
Усе цифрове обладнання сконструйоване з використанням невеликої
кількості основних схем, називаних логічними елементами, які виконують
деякі логічні функції із двійковими даними.
Існують два основні типи логічних схем: схеми прийняття рішень і
пам'ять. Логічні схеми прийняття рішень контролюють двійкові стани входів
і видають вихідний сигнал, заснований на станах входів і характеристиках
логічної схеми. Схеми пам'яті використовуються для зберігання двійкових
даних.
1. Логічні елементи
Розглянемо деякі логічні схеми.
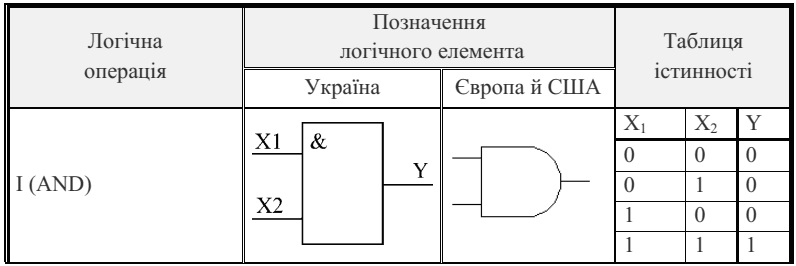
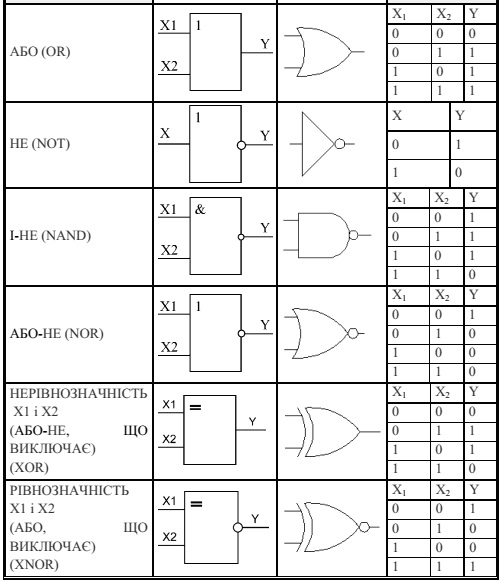
Елемент І - логічна схема, на виході якої 1 з'являється тільки тоді, коли
на всі його входи надходить сигнал 1. Якщо на який-небудь із входів надходить 0, на виході з'являється 0.
На мал. 1 показані стандартні позначення, використовувані для елементів
І. Елемент І може мати будь-яку кількість входів більше одного. Показані

позначення представляють найбільше часто використовувані елементи із двома, трьома й чотирма входами.
Стан і логічний зв'язок між вхідними й вихідними сигналами елемента І
відбиває так звана таблиця істинності (табл. 1), яка показує вихідний стан
двовходового елемента для будь-яких можливих станів входів: А і В - входи; Y- вихід.

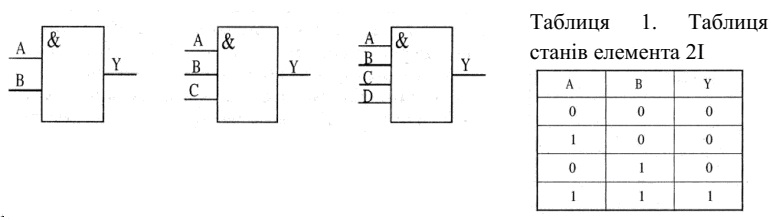
Мал. 1. Позначення елементів І

Елемент І виконує операцію логічного множення, яке відомо як функція І.
Елемент АБО - це логічна схема, на виході якої з'являється 1, якщо на
будь-який з його входів подано 1. На його виході з'являється 0, якщо на всі його входи подано 0. Цей елемент, як і елемент І, може мати два або більш входів.
На мал. 2 показані стандартні позначення, використовувані для елементів АБО із двома, трьома й чотирма входами.

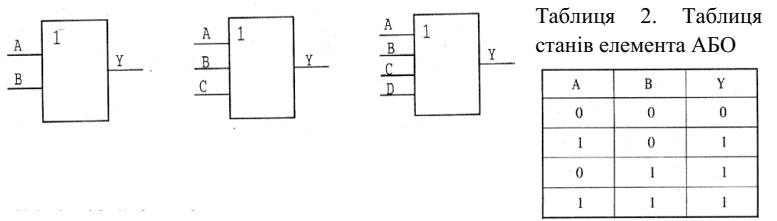
Мал. 2. Позначення елементів АБО

Значення на виході елемента АБО із двома входами наведені в табл. 2: А і
В - входи; Y - вихід.
Елемент АБО виконує логічну операцію додавання.
Елемент НЕ виконує функцію, яка називається інверсією. Мета інвертора - зробити стан виходу протилежним стану входу. Якщо на вхід інвертора поданий високий стан, або 1, то на виході з'явиться низький стан, або
0. Якщо ж на вхід інвертора подати низький стан, або 0, то на виході з'явиться високий стан, або 1.
Схематичне позначення інвертора показане на мал. 3.

Мал. 3. Позначення інвертора

Роботу інвертора відбиває табл. 3. Вхід інвертора позначений A , а вихід
- A (читається «не А»). Риска над буквою А показує заперечення А. Оскільки
інвертор має тільки один вхід, те можливі тільки два стани входу.
Елемент І-НЕ є комбінацією елементів І і НЕ й найбільше широко
використовуваною логічною функцією. Це обумовлене тим, що ці елементи
можуть бути використані для створення деяких інших логічних елементів.
Схематичне позначення елемента І-НЕ, а також його еквівалентність
послідовно включеним елементу І и інвертору, показані на мал. 4. Кружечок на виході позначає інвертування функції І.

Мал. 4. Елемент І-НЕ

Нижче наведена таблиця істинності для двухвходового елемента І-НЕ (табл. 4). Помітимо, що вихід елемента І-НЕ є запереченням виходу елемента І.
Подача 0 на будь-який вхід дає на виході 1.
Елемент АБО-НЕ є комбінацією елемента АБО й інвертора. Подібно
елементу І-НЕ, елемент АБО-НЕ також може бути використаний для створення інших логічних елементів. Схематичне позначення елемента АБО-НЕ, а також його еквівалентність послідовно включеним елементу АБО й інвертору показані на мал. 5. Кружечок на виході показує інвертування функції АБО.

Мал. 5. Елемент АБО-НЕ

Табл. 5 - таблиця істинності для двовходового елемента АБО-НЕ.
Помітимо, що його вихід є запереченням виходу елемента АБО. 1 на виході
з'являється тільки тоді, коли на обоє входу подано 0. Якщо на кожній із входів подано 1, то на виході буде 0. Існують елементи АБО-НЕ із двома, трьома, чотирма й вісьма входами.
Отримані про елементи відомості систематизуємо в таблиці 6.
Таблиця 6. Логічні елементи