Тема 6. Аналіз електронних кіл

4. Розв’язання рівнянь нелінійних електронних схем числовими методами

Оскільки найпростіша математична модель нелінійних резистивних схем є системою нелінійних алгебричних рівнянь стандартного вигляду (4.9), то для розв’язання її можна застосувати традиційні обчислювальні процедури, зокрема, метод Ньютона, чи метод простої ітерації.

            Метод простої ітерації реалізується згідно з такою ітераційною процедурою

                                                  ,                         (4.10)

– к-те наближення вектора змінних схеми, причому – початкове наближення, вибирається довільно, однак для того, щоб ітераційний процес згідно з (4.10) збігався, необхідно, щоб воно було доволі близько від розв’язку системи рівнянь (4.9).

            Ітераційний процес згідно з методом Ньютона є складнішим, водночас він має істотну перевагу перед методом простої ітерації, яка полягає у швидшій збіжності, а також менш жорстких вимогах до вибору початкового наближення.

            У разі розрахунку кола з одним нелінійним елементом система рівнянь (4.9) зводиться до одного рівняння з одним невідомим і тоді ітераційний процес реалізується згідно з такою формулою

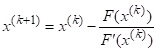               ,                                                  (4.11)

де   – похідна функції .

            Якщо ж у схемі, яка аналізується, є декілька нелінійних резисторів, тобто коли співвідношення (4.9) є системою нелінійних рівнянь, тоді запис рекурентної формули, що визначає ітераційний процес, є дещо іншим

                  ,                                      (4.12)

де  – матриця Якобі, або Якобіан, що визначається у такий спосіб:

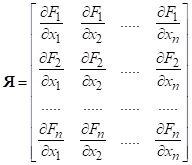                                                   .                                               (4.13)

            Як бачимо, рекурентні формули (4.10) – (4.12) є доволі зручними для комп’ютерної реалізації і це є основною причиною масового використання числових методів для аналізу нелінійних резистивних електронних схем.