Тема 6. Аналіз електронних кіл

3. Особливості розрахунку нелінійних резистивних кіл

Нелінійним електричним колом називається коло, в якому хоча би один елемент має нелінійну характеристику.

Складність аналізу таких кіл полягає у тому, що відповідні їм математичні моделі мають вигляд нелінійних рівнянь чи системи рівнянь, а як відомо, загальних методів аналітичного розв’язання таких рівнянь не існує. Тому для аналізу нелінійних електричних кіл, зокрема, резистивних використовують або графічні, або числові методи. Графічні методи є простими, не вимагають запису математичних моделей схем, однак їх можна ефективно застосовувати лише для аналізу доволі простих схем.

Основою числових методів аналізу є ті чи інші методи наближених обчислень, які потребують значних обчислювальних затрат. Причому розв’язок є сукупністю чисел, а не аналітичним виразом, що ускладнює його якісний аналіз. Однак універсальність названих методів та можливості простих комп’ютерних засобів зумовили нині їхнє широке використання.

 

 

 

Графічні методи

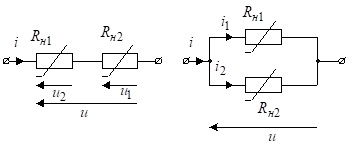
            Розглянемо побудову вольт-амперних характеристик з’єднаних нелінійних резисторів. Почнемо із розгляду елементарних способів з’єднання двох резисторів: послідовного та паралельного (рис.4.4)

Рис.4.4.  З’єднання двох нелінійних резисторів: а –  послідовне;

б – паралельне

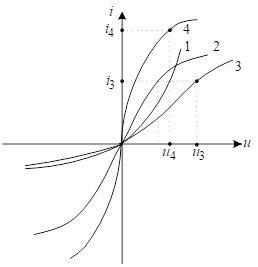
 Вольт-амперні характеристики (ВАХ) резисторів , показано на рис.4.5.

Враховуючи відомі співвідношення – для послідовного та – для паралельного з’єднання, можна сформулювати правила побудови ВАХ  послідовно чи паралельно з’єднаних резисторів.

 а) Послідовне з’єднання

При послідовному з’єднанні двох резисторів для одержання деякої точки ВАХ з’єднаних резисторів необхідно для вибраного значення струму провести горизонтальну пряму до перетину з ВАХ окремих резисторів і визначити на підставі точок перетину значення напруг на окремих резисторах. Графічно додавши ці величини, отримаємо значення напруги на послідовному з’єднанні, яке відкладаємо на проведеній раніше горизонтальній прямій. Так отримується точка  результуючої ВАХ.

Сказане  вище проілюстроване на рис.4.5, де ВАХ послідовного з’єднання резисторів зображене кривою 3.

 б) Паралельне з’єднання

 При паралельному з’єднанні двох резисторів для отримання   деякої точки ВАХ з’єднаних резисторів необхідно для вибраного значення напруги провести вертикальну пряму до перетину з ВАХ окремих резисторів і визначити на підставі точок перетину значення струмів через окремі резистори. Графічно додавши ці величини, одержимо значення струму в паралельному з’єднанні, яке відкладаємо на проведеній раніше вертикальній прямій. Так отримуємо точку  ВАХ паралельного з’єднання двох резисторів.

Результуюча ВАХ показана на рис.4.5 кривою 4.

 

Побудова кривої струму у нелінійному резисторі.

Суть цієї задачі полягає у графічній побудові часової залежності струму у нелінійному резистивному двополюснику , до якого прикладена змінна напруга . ВАХ резистивного елемента задається графічно. Сама процедура побудови показана на рис.4.6 і її часто називають методом трьох площин.

Перша координатна площина утворюється осями  і в цій площині відображається ВАХ заданого резистивного двополюсника.

Друга координатна площина утворена віссю , а також віссю , яка збігається з віссю  попередньої координатної площини. У цій площині будується графік змінної напруги, прикладеної до резистора.

Третя площина має координатні осі , причому вісь  збігається з віссю  першої координатної площини і вони слугують для відображення графіка струму у резистивному двополюснику.

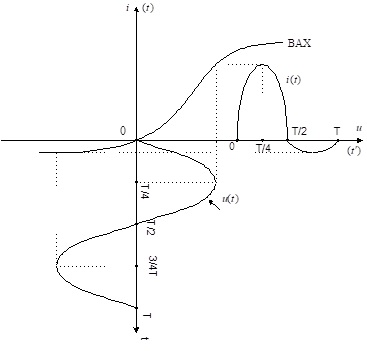
Рис.4.6. Ілюстрація методу трьох площин

 

Процедура побудови кривої струму, як це видно з рис.4.6, полягає у тому, що спочатку для заданого момента часу  знаходять значення напруги, прикладеної до резистора , а після цього, проектуючи це значення на графік ВАХ, отримують значення струму в той самий момент часу, який відображається на осі

 

2.2. Числові методи розрахунку нелінійних резистивних схем

Як уже було сказано вище, суть числових методів полягає у наближеному розв’язанні математичної моделі нелінійного кола. Тому детальніше розглянемо формування математичної моделі нелінійної резистивної схеми.

 

Математична модель схеми з одним нелінійним резистором

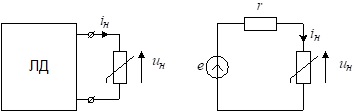
У такому разі нелінійну схему зручно подати так, як зображено на рис.4.7.

Рис.4.7.  Подання електричної схеми з одним нелінійним резистором

 

Двополюсник ЛД, показаний на рисунку, містить всі лінійні елементи схеми, тобто на підставі методу еквівалентного генератора він може бути поданий неідеальним джерелом ЕРС з параметрами , які легко розрахувати.

Аналізуючи спрощену схему (рис.4.7, б), на підставі другого закону Кірхгофа можна записати рівняння

                       ,                                                           (4.4)

або, врахувавши рівняння ВАХ нелінійного резистора , отримаємо математичну модель у такому вигляді:

                                                                             (4.5)

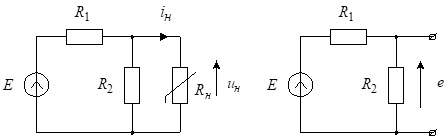
Приклад 4.2. Записати математичну модель такої нелінійної резистивної схеми. 

    

Рис.4.8. Схема до прикладу 4.2

 

Неважко переконатись, що параметри еквівалентного генератора двополюсника рис.4.2, б такі

                                                         .

            Тоді згідно з (4.5) математична модель заданої схеми матиме вигляд:

                                                .

Побудова математичних моделей резистивної схеми із декількома нелінійними елементами

            Будь-яку електричну схему з декількома нелінійними резисторами можна подати у такому вигляді, зображеному на рис. 4.9.

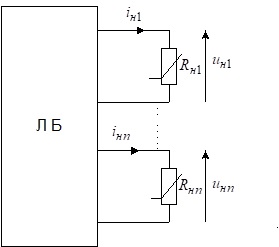
Рис.4.9.  Подання резистивної схеми з - нелінійними резисторами

 

            На рис.4.9 ЛБ є лінійним резистивним багатополюсником, тобто його можна описати, зокрема, рівнянням в - параметрах  (2.43)

               ,                                                             (4.6)

де – вектори струмів та напруг лінійного багатополюсника; – вектор вільних струмів багатополюсника ; – матриця –параметрів багатополюсника. Очевидно, що струми та напруги багатополюсника є одночасно струмами та напругами нелінійних резисторів.

            ВАХ нелінійних резисторів можна записати також у вигляді векторного співвідношення

                 ,                                                   (4.7)

де

є деякою вектор-функцією, компонентами якої є вирази ВАХ окремих нелінійних резисторів.

Підставивши вираз (4.7) у рівняння (4.6), отримаємо математичну модель цієї схеми у матричному записі:

                                            .                                     (4.8)

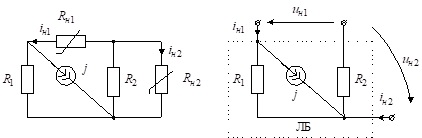
Приклад 4.3. Запишемо математичну модель схеми, показаної на рис. 4.10.

Рис.4.10. Схема до прикладу 4.3

            Запишемо рівняння в –параметрах лінійного триполюсника ЛБ стосовно напруг, показаних на рис.4.10, б.

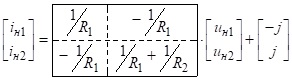
З урахуванням виразів ВАХ нелінійних резисторів

 математична модель схеми (рис.4.10, а) матиме такий вигляд

.

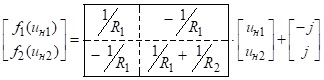Підсумувавши матеріал цього параграфа, що математичну модель нелінійних резистивних кіл можна подати у такому вигляді

                     ,                           (4.9)

де – вектор змінних схеми; як правило, це струми чи напруги нелінійних резисторів; – це деяка нелінійна вектор-функція.