Тема 1. Основні поняття теорії сигналів

8. Амплітудно-модульовані сигнали

Математичну модель АМ-сигналу можна записати в загальному вигляді:

s_АМ(t)=A_m(t)cos(w₀t+j₀), (1.43)

де A_m(t) – функція, яка описує закон зміни амплітуди неперервного несучого коливання в часі. Ця функція повинна бути повільною порівняно з cos(w₀t+j₀), так, що за час, протягом якого повна фаза (w₀t+j₀) зміниться на 2p, функцію A_m(t) можна вважати сталою. Функцію A_m(t) називають обгинаючою (обвідною) АМ-сигналу. Математично її описують виразом:

(1.44)

Математична модель АМ-сигналу описує зміну амплітуди несучого коливання під дією інформаційного сигналу.

де A_m0 – амплітуда немодульованого (несучого) коливання, яка входить у (1.42); k – коефіцієнт пропорційності; u(t) – модулюючий (керуючий) сигнал.

Із (1.44) бачимо, що обгинаюча АМ-сигналу змінюється пропорційно до модулюючого сигналу u(t) стосовно амплітуди несучого коливання.

Формування АМ-сигналу зображено на рис.1.12.

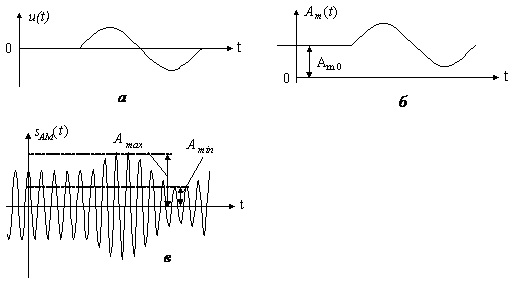
Рис.1.12. Формування АМ-сигналу: а – модулюючий сигнал;
б –- обгинаюча АМ-сигналу; в – АМ-сигнал

Забезпечення пропорційної залежності між обгинаючою АМ-сигналу та керуючим інформаційним сигналом – умова відсутності спотворень при амплітудній модуляції.

З урахуванням (1.44) математичну модель АМ-сигналу можна записати:

(1.45)

звідки випливає, що між миттєвими значеннями модулюючого сигналу u(t) та обгинаючої A_m(t) існує однозначний пропорційний зв’язок за умови:

. (1.46)

Якщо умова (1.46) не виконуєься, то форма обгинаючої A_m(t) та модулюючого сигналу u(t) не збігаються – виникає небажане явище спотворення обгинаючої АМ-сигналу.

Основним параметром АМ-сигналу є коефіцієнт модуляції, який визначають як відношення максимального відхилення амплітуди модульованого сигналу стосовно амплітуди несучого (немодульованого) коливання до амплітуди несучого коливання:

Очевидно, що спотворення обгинаючої A_m(t) АМ-сигналу відсутні, якщо виконується умова:

0<m<=1.