Тема 1. Основні поняття теорії сигналів

4. Часовий (динамічний) опис сигналів

              Часовий (динамічний) опис сигналів            

Як елементарні сигнали у часовому описі складних сигналів використовують одиничний стрибок та дельта-імпульс.

                Одиничний стрибок (функція Хевісайда) загалом задається виразом:

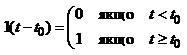                                                             (1.21)

                Застосування одиничного стрибка для математичного опису аналогових сигналів полягає в тому, що спочатку замінюють (апроксимують) аналоговий сигнал s(t) ступінчатим сигналом     , який утворюється як сума вписаних у сигнал s(t) та зміщених на Dt елементарних стрибкоподібних сигналів, амплітуди яких пропорційні до деяких вагових коефіцієнтів Ds_k (див. рис. 1.4).

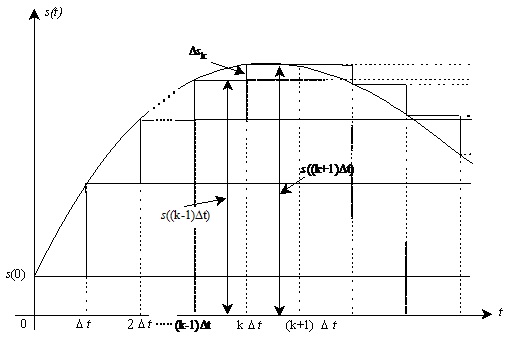
Рис.1.4. Заміна аналогового сигналу ступінчатим

                Як видно з рис. 1.4, значення вагових коефіцієнтів Ds_k у моменти часу t_k=kDt дорівнюють різниці відліків сигналу s(t) у поточний і попередній моменти часу:

Ds_k=s(t_k)- s(t_k-1)=s(kDt)-s((k-1) Dt)

                Поточне значення сигналу s(t) у довільний момент t£NDt наближено описує вираз:

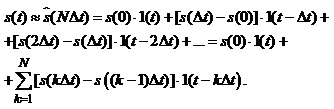                                    (1.22)

                Похибка апроксимації сигналу s(t) ступінчастим сигналом 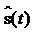  буде зменшуватись зі зменшенням інтервалу Dt і у граничному випадку (Dt->0) сигнали s(t) та 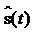 будуть збігатися. У такому разі динамічну модель аналогового сигналу s(t), поданого через функції Хевісайда, отримуємо із (1.22) заміною дискретної змінної kDt неперервною змінною t, малих приростів [s(kDt)-s((k-1)Dt)] – диференціалом  , знака суми – інтегралом:

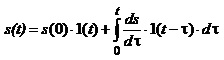                                                      (1.23)

                        Інший спосіб математичного опису аналогового сигналу ґрунтується на використанні дельта-імпульсу (функції Дірака), який в загальному випадку задається виразом:

                                                                (1.24)

                Дельта-імпульс є імпульсом нескінченно короткої тривалості з нескінченно великою амплітудою та площею, що дорівнює одиниці, тобто

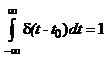                                                                                    (1.25)

                Функція Дірака є похідною від функції Хевісайда, а функція Хевісайда – інтегралом від функції Дірака:

                                                                       (1.26)

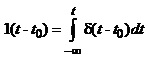                                                                       (1.27)

                Використовуючи дельта-імпульс, аналоговий сигнал s(t) апроксимують сигналом 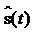, що утворений зміщеними в часі на інтервали Dt прямокутними імпульсами заввишки s_k=s(t_k)=s(kDt)  та тривалістю Dt, як показано на рис.1.5

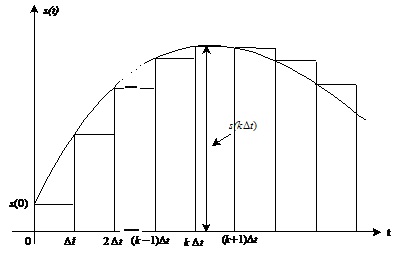
Рис.1.5. Апроксимація аналогового сигналу послідовністю прямокутних імпульсів

 

                Розглядаючи кожний елементарний імпульс як різницю двох стрибків, зсунутих у часі один відносно одного на інтервал Dt, можемо наближено записати поточне значення сигналу s(kDt) в інтервалі kDt£t<(k+1)Dt у вигляді:

а для сигналу загалом:

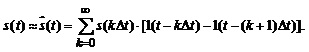                                          (1.28)

                Похибка апроксимації s(t) сигналом 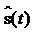 буде зменшуватися у разі зменшення інтервалу Dt. У граничному випадку  (Dt->0), замінюючи у (1.28) дискретну змінну kDt неперервною змінною t, знак суми – інтегралом, та враховуючи (1.26), отримуємо динамічну модель аналогового сигналу з використанням дельта-функції:

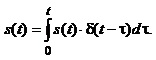                                                                       (1.29)

                Примітка: для одержання формули (1.29) використано  співвідношення:

                На закінчення зауважимо, що подання складного сигналу сукупністю елементарних однотипних сигналів дає змогу застосувати для  аналізу електричних кіл принцип накладання (суперпозиції), згідно з яким реакція лінійного електричного кола на дію цього складного сигналу дорівнює сумі реакцій, викликаних кожним елементарним сигналом. Використання цього принципу істотно полегшує аналіз електричних кіл і є основою багатьох поширених методів аналізу.