Тема 1. Основні поняття теорії сигналів
Тема 1. Основні поняття теорії сигналів – 4 год.
1. Класифікація та способи математичного опису сигналів
2. Аналогові сигнали
2.1. Частотний (спектральний) опис сигналів
2.2. Часовий (динамічний) опис сигналів
2.3. Операторний опис сигналів
3. Дискретизовані та цифрові сигнали
4. Модульовані сигнали та їхнє
застосування
4.2. Сигнали
з кутовою модуляцією (ЧМ- та ФМ-сигнали)
5.1. Числові
характеристики випадкових сигналів
4.1. Амплітудно-модульовані сигнали
4.3. Модуляція імпульсних коливань
5. Стохастичні (випадкові) сигнали
3. Частотний (спектральний) опис сигналів
Вище зазначалось, що елементарним сигналом, який використовують при спектральному описі сигналів, є гармонічний сигнал, що задається виразом:
Гармонічне коливання – елементарний сигнал, який використовують при частотному (спектральному) описі складних сигналів.
s(t)=Amcos(wt+j)=Amcosy(t), (1.1)
де Am – амплітуда (максимальне відхилення від нульового значення), розмірність якої збігається з розмірністю сигналу;
w – кутова швидкість, яку вимірюють у радіанах за секунду;
j – початкова фаза, яку вимірюють в кутових одиницях (радіанах або градусах).
Аргумент гармонічного сигналу y(t) =wt+j називають повною фазою.
Гармонічний сигнал належить до неперервних у часі сигналів, які теоретично існують на необмеженому часовому інтервалі (-¥<t<¥), і задовольняють умову періодичності, тобто повторення миттєвих значень через певний проміжок часу, який називають періодом:
s(t)=s(t±nТ), (1.2)
де Т – період сигналу, n – довільне ціле число.
Оскільки за період відбувається зміна повної фази на 2p радіанів, то звідси випливає відоме співвідношення:
Т=2p/w=1/f, (1.3)
де f – частота коливань, яку вимірюють у герцах [Гц], і яка пов’язана з кутовою швидкістю w співвідношенням: w=2pf.
Зауважимо, що кутову швидкість w часто називають кутовою частотою або просто частотою, і надалі будемо теж користуватись цим терміном.
Гармонічні сигнали мають цікаву властивість: похідна та інтеграл від гармонічного сигналу теж є гармонічним сигналом з тією самою частотою, амплітуда якого залежить від частоти, а початкова фаза зсунута на p/2 відносно фази первинного сигналу.
Гармонічний (частотний) спектр складного сигналу – подання цього сигналу сумою елементарних гармонічних коливань.
Суть спектрального опису складних сигналів полягає у тому, що їх подають у вигляді нескінченної суми елементарних гармонічних сигналів з різними амплітудами, частотами та початковими фазами.
Сукупність усіх елементарних гармонічних сигналів, які в сумі утворюють заданий складний сигнал, називають спектром цього сигналу у базисі гармонічних коливань.
Так, складний сигнал який періодично повторюється з частотою w0=2p/Т0, (де Т0=1/f0 – період повторення), можна описати рядом Фур’є у тригонометричній формі у базисі гармонічних функцій з кратними частотами:
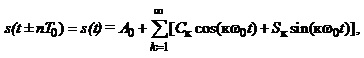 (1.4a)
(1.4a)
або в компактнішій формі:
Ряд Фур’є – спектральний опис складного періодичного сигналу.
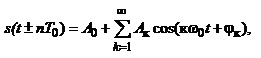 (1.4б)
(1.4б)
де А0 – постійна складова (середнє значення сигналу за період);
Ск та Sк – амплітуди косинусних та синусних складових к-го порядкового номера;
Ак, jк – амплітуда та початкова фаза к-ї гармонічної складової.
Ці величини визначають на підставі формул:
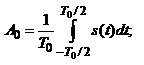 (1.5)
(1.5)
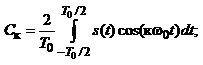 (1.6)
(1.6)
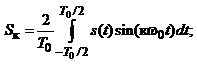 (1.7)
(1.7)
Амплітуду Ак та початкову фазу jк к-ї гармонічної складової визначають через Ск та Sк:
![]() (1.8)
(1.8)
jк = – arc tg(Sк/Cк). (1.9)
Зауважимо, що вирази (1.4а) та (1.4б) справедливі, якщо функція s(t) задовольняє умови Діріхле, тобто протягом періоду вона може мати скінченну кількість розривів першого роду, а також скінченну кількість максимумів та мінімумів і задовольняє умову абсолютної інтегрованості:
Практично усі реальні сигнали задовольняють умови Діріхле, тому на практиці при спектральному поданні сигналів ці умови спеціально не акцентують.
Спектри періодичних сигналів є дискретними (лінійчастими).
Отже, вирази (1.4а, 1.4б) описують спектр складного періодичного сигналу, який в загальному випадку складається з постійної складової А0 та нескінченної кількості гармонічних складових, частоти яких становлять дискретний ряд значень kw0 (k=1,2,3,...), кратних основній частоті w0 . Ці складові називають гармоніками періодичного сигналу. Спектр, який складається з окремих складових, називають дискретним або лінійчастим. Гармоніку, яка відповідає номерові k=1, називають першою або основною гармонікою.
Амплітудний та фазовий спектр – дві основні характеристики сигналів.
У загальному випадку гармоніки, які входять до складу спектра, мають різні амплітуди та початкові фази. Щоб отримати наочне уявлення про спектр сигналу, використовують графічне зображення спектра у вигляді двох спектральних діаграм: амплітудної та фазової. Будуючи їх, на осі абсцис відкладають частоту, а на осі ординат – відповідно величини амплітуд Ак гармонік та їхні початкові фази jк.
На рис.1.2 для прикладу зображено амплітудну (а) та фазову (б) спектральні діаграми періодичного сигналу, поданого на рис. 1.2, в.
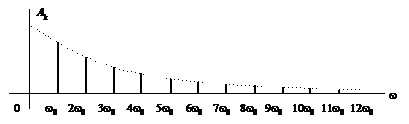
а
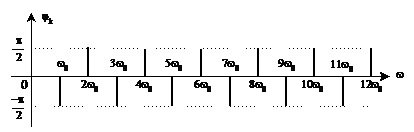
б
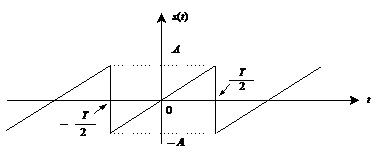
в
Рис.1.2. Амплітудна (а) та фазова (б)
спектральні діаграми періодичного сигналу (в), який повторюється з частотою ![]()
Із спектральних діаграм видно, що відстань між двома сусідніми гармоніками по осі частот (тобто відстань між вертикальними лініями) дорівнює значенню частоти повторення w0 періодичного сигналу. Це означає, що зі збільшенням частоти w0 повторення або зменшенням періоду Т0 сигналу відстань між вертикальними лініями на спектральних діаграмах збільшується (спектр стає рідшим, але займає ширший діапазон частот) і навпаки. Крім того, як випливає з виразів (1.5) – (1.7), зміна частоти повторення (або періоду) сигналу впливає також і на величину амплітуд гармонік.
Згадану властивість спектра періодичного сигналу зручно використати під час визначення спектрів імпульсних сигналів, які не є періодичними.
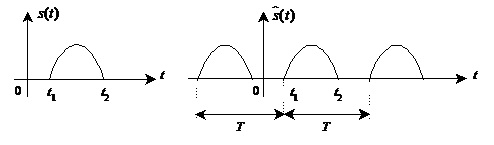
Приймемо, що імпульсний сигнал s(t) має форму поодинокого імпульсу (рис.1.3, а), який відрізняється від нуля на часовому проміжку (t1, t2).
|
а |
б |
Рис.1.3. До спектрального аналізу імпульсного сигналу
Імпульсний (поодинокий) сигнал як граничний випадок періодичного сигналу при Т®¥.
Перетворимо заданий
поодинокий імпульс на періодичний сигнал ![]() повторенням
його з довільним періодом T>(t2-t1), як показано на рис.1.3, б. Отриману періодичну
функцію
повторенням
його з довільним періодом T>(t2-t1), як показано на рис.1.3, б. Отриману періодичну
функцію ![]() розкладемо
в ряд Фур’є, причому коефіцієнти А0,
Ак, Ск, Sк
будуть тим меншими, чим більшим буде вибрано інтервал Т як період. Це випливає з виразів (1.5) – (1.7). Якщо період Т збільшувати до нескінченності, то всі
імпульси, крім первинного, змістяться у нескінченність і залишиться лише
первинний імпульс s(t).
розкладемо
в ряд Фур’є, причому коефіцієнти А0,
Ак, Ск, Sк
будуть тим меншими, чим більшим буде вибрано інтервал Т як період. Це випливає з виразів (1.5) – (1.7). Якщо період Т збільшувати до нескінченності, то всі
імпульси, крім первинного, змістяться у нескінченність і залишиться лише
первинний імпульс s(t).
Отже,
![]() (1.10)
(1.10)
При тому одержимо нескінченно малі амплітуди гармонічних складових, сума яких дає початкову неперіодичну функцію s(t), задану в інтервалі (t1, t2).
Оскільки при Т®¥ основна частота функції w0=(2p/Т) ®0, то це означає, що відстань по осі частот між спектральними лініями на спектральних діаграмах (яка дорівнює основній частоті w0) стає нескінченно малою, а спектр – суцільним. Отже, доходимо висновку, що при спектральному поданні імпульсних неперіодичних сигналів отримуємо суцільний спектр, який складається з нескінченно великої кількості гармонічних коливань з нескінченно малими амплітудами, частота яких неперервно змінюється від нуля до нескінченності.
Опишемо сказане
математично. Амплітуди косинусних та
синусних складових к-ї гармоніки
періодичного сигналу ![]() записуємо
виразами:
записуємо
виразами:
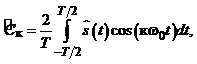 (1.11)
(1.11)
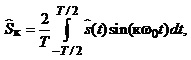 (1.12)
(1.12)
де w0=2p/Т.
Якщо Т зростає до нескінченності, то частота w0 прямуватиме до нуля, і її необхідно замінити нескінченно малою величиною dw. Крім того, добуток кw0 може набувати довільних значень і стане неперервною (а не дискретною) функцією к, тому величину кw0 необхідно розглядати як неперервну змінну частоту w, яка змінюється від нуля до нескінченності.
Враховуючи це, отримуємо вирази для малих амплітуд косинусних та синусних складових:
Косинус - перетворення та синус - перетворення Фур’є – складові спектральної характеристики імпульсних сигналів.
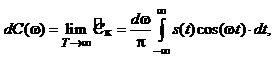 (1.13)
(1.13)
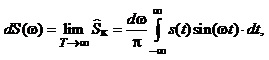 (1.14)
(1.14)
Введемо позначення:
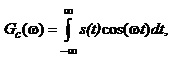 (1.15)
(1.15)
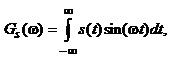 (1.16)
(1.16)
Формули (1.15) та (1.16) називають відповідно косинус-перетворенням Фур’є та синус-перетворенням Фур’є.
Результуючі амплітуди складових спектра на довільній частоті w дорівнюють:
![]() (1.17)
(1.17)
а їхні початкові фази:
Спектральна густина – основна спектральна характеристика імпульсних сигналів.
![]() (1.18)
(1.18) ![]() (1.19)
(1.19)
Функцію G(w) називаюь модулем спектральної густини, що описує амплітудний спектр імпульсного сигналу, а функцію y(t), яка описує фазовий спектр цього сигналу, називають аргументом спектральної густини.
Зауважимо, що спектральна густина – не спектр, а лише спектральна характеристика імпульсного сигналу, оскільки на конкретній частоті амплітуда відповідної спектральної складової дорівнює нулеві.
Отже, імпульсний (неперіодичний) сигнал – це сукупність нескінченної кількості гармонічних складових із нескінченно малими амплітудами dA(w), початковими фазами y(w), частота яких неперервно змінюється від нуля до нескінченності, що математично можна записати так:
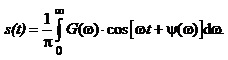 (1.20)
(1.20)