Тема 1. Основні поняття теорії сигналів
| Сайт: | Освітній сайт КНУБА |
| Курс: | Основи теор. кіл, сигнали та проц. в електроніці БІКС |
| Книга: | Тема 1. Основні поняття теорії сигналів |
| Надрукував: | Гість-користувач |
| Дата: | пʼятниця, 26 квітня 2024, 20:06 |
Опис
Тема 1. Основні поняття теорії сигналів – 4 год.
1. Класифікація та способи математичного опису сигналів
2. Аналогові сигнали
2.1. Частотний (спектральний) опис сигналів
2.2. Часовий (динамічний) опис сигналів
2.3. Операторний опис сигналів
3. Дискретизовані та цифрові сигнали
4. Модульовані сигнали та їхнє
застосування
4.2. Сигнали
з кутовою модуляцією (ЧМ- та ФМ-сигнали)
5.1. Числові
характеристики випадкових сигналів
4.1. Амплітудно-модульовані сигнали
4.3. Модуляція імпульсних коливань
5. Стохастичні (випадкові) сигнали
Зміст книги
- 1. Класифікація та способи математичного опису сигналів
- 2. Аналогові сигнали
- 3. Частотний (спектральний) опис сигналів
- 4. Часовий (динамічний) опис сигналів
- 5. Операторний опис сигналів
- 6. Дискретизовані та цифрові сигнали
- 7. Модульовані сигнали та їх застосування
- 8. Амплітудно-модульовані сигнали
- 9. Сигнали з кутовою модуляцією (ЧМ- та ФМ-сигнали)
- 10. Модуляція імпульсних коливань
- 11. Стохастичні (випадкові) сигнали
- 12. Числові характеристики випадкових сигналів
1. Класифікація та способи математичного опису сигналів
Електричний сигнал як матеріальний носій інформації, являє собою певну змінну фізичну величину (напругу, струм, заряд, магнітний потік), яку називають коливанням.
Розрізняють дві основні групи сигналів: детерміновані та випадкові (стохастичні).
Детермінованими називають такі сигнали, значення яких у будь-який момент часу є точно відоме, тобто їх можна передбачити безпомилково. Такі сигнали не несуть нової інформації, проте їх використовують як тестові сигнали при дослідженні різних електронних кіл та пристроїв.
Випадковими називають такі сигнали, значення яких у будь-який момент часу неможливо передбачити абсолютно точно. Випадковими сигналами є різноманітні електромагнітні коливання атмосферного та промислового походження, а також сигнали інших передавальних станцій, які перешкоджають прийманню інформаційних сигналів. Отже, випадкові сигнали можна поділити на корисні та завади (шуми).
Детерміновані та випадкові сигнали - дві основні групи сигналів.
Зауважимо, що поділ усієї розмаїтості сигналів на детерміновані та випадкові є відносним. Наприклад, корисний сигнал, прийнятий на приймальному пункті, є для адресата випадковим, бо адресат наперед не знає змісту інформації, яку несе даний сигнал. У той же час цей сигнал на передавальному пункті вважається детермінованим, оскільки там точно відома інформація, яку несе сигнал.
Сигнали також прийнято класифікувати залежно від характеру зміни в часі та на множині значень.
Розрізняють сигнали неперервні та дискретні в часі. Неперервні в часі сигнали існують у кожен момент часу. Дискретні в часі сигнали появляються лише в певні моменти часу.
Крім того, розрізняють сигнали неперервні та дискретні на множині значень. Неперервні на множині значень сигнали можуть приймати неперервну множину значень (континуум значень) у заданому інтервалі, тобто їх миттєві значення можуть змінюватись плавно, хоча також можуть мати окремі стрибки. Дискретні на множині значень сигнали можуть приймати лише дискретні значення у заданому інтервалі, тобто їх миттєві значення можуть змінюватись лише стрибкоподібно.
На підставі цієї класифікації можна виділити такі чотири типи сигналів:
1. Аналогові або континуальні - неперервні в часі та на множині значень.
2.Дискретизовані - дискретні в часі та неперервні на множині значень.
3. Квантовані - неперервні в часі та дискретні на множині значень.
4. Цифрові - дискретні одночасно в часі та на множині значень.
Отже, будь-яке первинне повідомлення може бути перетворене у будь-який із чотирьох наведених вище типів сигналів. Наприклад, первинне повідомлення у вигляді неперервного звукового сигналу можна перетворити:
а) в аналоговий електричний сигнал sA(t), миттєві значення якого пропорційні силі звуку (рис.1.1а);
б) у дискретизований сигнал sД(t), який є послідовністю коротких імпульсів, амплітуди яких пропорційні силі звуку в дискретні моменти часу (рис.1.1 б);
в) у квантований сигнал sк(t), який є послідовністю стрибкоподібних змін з дозволеними фіксованими значеннями, що відповідають миттєвим значенням звукового сигналу з деякою допустимою похибкою (рис.1.1 в);
г) у цифровий сигнал sц(t), який є послідовністю коротких імпульсів, амплітуди яких можуть приймати дозволені фіксовані значення, що відповідають миттєвим значенням звукового сигналу з певною допустимою похибкою (рис.1.1 г).
Первинне повідомлення можна перетворити в один із чотирьох можливих типів сигналів: аналоговий, дискретизований, квантований, цифровий.
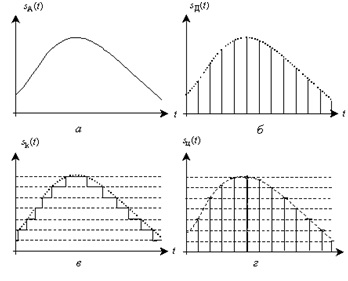
Рис.1.1 Аналоговий (а), дискретизований (б), квантований (в) та цифровий (г) сигнали, які відповідають одному й тому ж первинному повідомленню
Найбільш поширеними є аналогові та цифрові сигнали. Способи реалізації операцій пересилання, обробки, зберігання та відтворення інформації, представленої аналоговими та цифровими сигналами, докорінно різняться між собою, тому в інформаційній електроніці можна виділити два напрями - аналогову та цифрову електроніку, які займаються способами технічної реалізації, принципами побудови та методами проектування пристроїв і систем, які здійснюють різноманітні операції відповідно над аналоговими і цифровими сигналами.
Аналогова та цифрова електроніка - два напрями інформаційної електроніки.
Залежно від тривалості проміжку часу, протягом якого існує сигнал, розрізняють неперервні (довготривалі) та імпульсні сигнали.
Неперервні сигнали теоретично існують на нескінченному проміжку часу. Реальні сигнали мають початок і кінець і їх не можна вважати неперервними. Проте в багатьох випадках достатньо довготривалі сигнали вважають неперервними.
Імпульсні сигнали (одинокі імпульси) існують лише протягом короткого проміжку часу, а в усі інші моменти їх значення тотожно дорівнюють нулеві.
Всі реальні фізичні сигнали є дійсними функціями часу, але залежно від потреб методів аналізу найчастіше використовують такі способи їх математичного опису:
а) опис сигналу як функції часу - часовий опис;
б) опис сигналу як деякої функції частоти - частотний (спектральний) опис;
в) опис сигналу в операторній формі - операторний опис.
У багатьох випадках для спрощення аналізу проходження сигналів через електронні кола доцільно описати сигнал як сукупність вибраних певним чином елементарних (найпростіших) сигналів. До елементарних сигналів належать: гармонічне коливання, одиничний стрибок (функція Хевісайда), дельта-імпульс (функція Дірака). Гармонічне коливання використовують при частотному (спектральному) описі сигналів, а одиничний стрибок та дельта-імпульс - при часовому описі, який інколи називають динамічним описом.
Способи
математичного опису реальних сигналів:
- часовий
- частотний
- операторний.
2. Аналогові сигнали
У
цьому підрозділі розглянемо способи математичного опису детермінованих
аналогових сигналів, які найчастіше використовують для аналізу їхнього
проходження через електронні кола.
Ана́логовий сигна́л — сигнал (напруга, струм тощо), неперервний на всьому
проміжку часу. Аналоговий сигнал є або вираженим синусоїдальним коливанням, або, у загальному випадку,
розкладеним у ряд (Фур'є) накладанням синусоїдальних коливань певної амплітуди і частоти. Протилежністю аналоговим
сигналам є дискретний сигнал, який має обмежені часові рамки (дискрета, імпульс). Аналоговий сигнал є традиційним для використання у
радіо-телекомунікаційних системах, системах автоматичного керування тощо. При передачі інформації аналоговим сигналом, його видозміна можлива шляхом зміни частоти чи амплітуди коливань. Перевагою аналогового сигналу над
дискретним є відсутність невизначеності між відліками, яку має дискретний
сигнал. Аналоговий
сигнал використовує певні властивості середовища для передачі інформації.
Наприклад, анаероїдний
барометр використовує поворотну позицію як сигнал для передачі інформації про тиск.
В електричних сигналах для передачі інформації, може змінюватися напруга, струм, фаза або частота сигналу. Будь-яка
інформація може передаватися в формі аналогового сигналу; часто такий сигнал це
виміряна реакція на зміну фізичного явища, такого як звук, світло, температура, позиція, або тиск. Фізична величина
перетворюється на аналоговий сигнал за допомогою перетворювача. Наприклад, при записуванні звуку,
коливання тиску повітря, що діє на діафрагму мікрофона яка приводить до відповідних
коливань струму, що створюється котушкою електромагнітного мікрофону, або
напруги, яку створює конденсаторний мікрофон. Теоретично
аналоговий сигнал має нескінченну роздільну здатність. На практиці аналоговий
сигнал піддається електронному
шуму і спотворенню, що спричинені каналами передачі і операцій з обробки сигналів, що можуть значно погіршити співвідношення сигнал-шум (SNR). Перетворення аналогового
сигналу в цифрову форму породжує постійний шум низького рівня, який називають шумом квантування, але якщо сигнал уже перетворено в
цифрову форму в основному він може передаватися або оброблятися без появи
додаткового шуму або спотворення. В аналогових системах, важко встановити коли
така деградація відбулася. Однак, в цифрових системах, деградацію можна не лише
виявити але і виправити.
3. Частотний (спектральний) опис сигналів
Вище зазначалось, що елементарним сигналом, який використовують при спектральному описі сигналів, є гармонічний сигнал, що задається виразом:
Гармонічне коливання – елементарний сигнал, який використовують при частотному (спектральному) описі складних сигналів.
s(t)=Amcos(wt+j)=Amcosy(t), (1.1)
де Am – амплітуда (максимальне відхилення від нульового значення), розмірність якої збігається з розмірністю сигналу;
w – кутова швидкість, яку вимірюють у радіанах за секунду;
j – початкова фаза, яку вимірюють в кутових одиницях (радіанах або градусах).
Аргумент гармонічного сигналу y(t) =wt+j називають повною фазою.
Гармонічний сигнал належить до неперервних у часі сигналів, які теоретично існують на необмеженому часовому інтервалі (-¥<t<¥), і задовольняють умову періодичності, тобто повторення миттєвих значень через певний проміжок часу, який називають періодом:
s(t)=s(t±nТ), (1.2)
де Т – період сигналу, n – довільне ціле число.
Оскільки за період відбувається зміна повної фази на 2p радіанів, то звідси випливає відоме співвідношення:
Т=2p/w=1/f, (1.3)
де f – частота коливань, яку вимірюють у герцах [Гц], і яка пов’язана з кутовою швидкістю w співвідношенням: w=2pf.
Зауважимо, що кутову швидкість w часто називають кутовою частотою або просто частотою, і надалі будемо теж користуватись цим терміном.
Гармонічні сигнали мають цікаву властивість: похідна та інтеграл від гармонічного сигналу теж є гармонічним сигналом з тією самою частотою, амплітуда якого залежить від частоти, а початкова фаза зсунута на p/2 відносно фази первинного сигналу.
Гармонічний (частотний) спектр складного сигналу – подання цього сигналу сумою елементарних гармонічних коливань.
Суть спектрального опису складних сигналів полягає у тому, що їх подають у вигляді нескінченної суми елементарних гармонічних сигналів з різними амплітудами, частотами та початковими фазами.
Сукупність усіх елементарних гармонічних сигналів, які в сумі утворюють заданий складний сигнал, називають спектром цього сигналу у базисі гармонічних коливань.
Так, складний сигнал який періодично повторюється з частотою w0=2p/Т0, (де Т0=1/f0 – період повторення), можна описати рядом Фур’є у тригонометричній формі у базисі гармонічних функцій з кратними частотами:
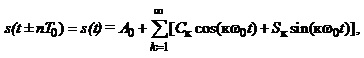 (1.4a)
(1.4a)
або в компактнішій формі:
Ряд Фур’є – спектральний опис складного періодичного сигналу.
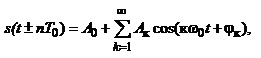 (1.4б)
(1.4б)
де А0 – постійна складова (середнє значення сигналу за період);
Ск та Sк – амплітуди косинусних та синусних складових к-го порядкового номера;
Ак, jк – амплітуда та початкова фаза к-ї гармонічної складової.
Ці величини визначають на підставі формул:
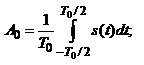 (1.5)
(1.5)
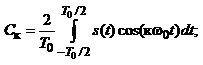 (1.6)
(1.6)
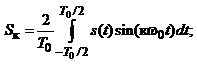 (1.7)
(1.7)
Амплітуду Ак та початкову фазу jк к-ї гармонічної складової визначають через Ск та Sк:
![]() (1.8)
(1.8)
jк = – arc tg(Sк/Cк). (1.9)
Зауважимо, що вирази (1.4а) та (1.4б) справедливі, якщо функція s(t) задовольняє умови Діріхле, тобто протягом періоду вона може мати скінченну кількість розривів першого роду, а також скінченну кількість максимумів та мінімумів і задовольняє умову абсолютної інтегрованості:
Практично усі реальні сигнали задовольняють умови Діріхле, тому на практиці при спектральному поданні сигналів ці умови спеціально не акцентують.
Спектри періодичних сигналів є дискретними (лінійчастими).
Отже, вирази (1.4а, 1.4б) описують спектр складного періодичного сигналу, який в загальному випадку складається з постійної складової А0 та нескінченної кількості гармонічних складових, частоти яких становлять дискретний ряд значень kw0 (k=1,2,3,...), кратних основній частоті w0 . Ці складові називають гармоніками періодичного сигналу. Спектр, який складається з окремих складових, називають дискретним або лінійчастим. Гармоніку, яка відповідає номерові k=1, називають першою або основною гармонікою.
Амплітудний та фазовий спектр – дві основні характеристики сигналів.
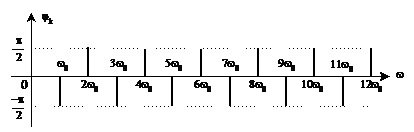
У загальному випадку гармоніки, які входять до складу спектра, мають різні амплітуди та початкові фази. Щоб отримати наочне уявлення про спектр сигналу, використовують графічне зображення спектра у вигляді двох спектральних діаграм: амплітудної та фазової. Будуючи їх, на осі абсцис відкладають частоту, а на осі ординат – відповідно величини амплітуд Ак гармонік та їхні початкові фази jк.
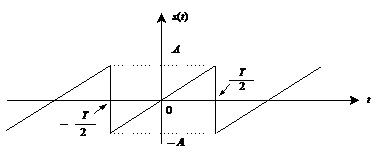
На рис.1.2 для прикладу зображено амплітудну (а) та фазову (б) спектральні діаграми періодичного сигналу, поданого на рис. 1.2, в.
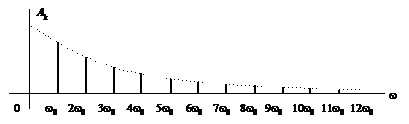
а
б
в
Рис.1.2. Амплітудна (а) та фазова (б)
спектральні діаграми періодичного сигналу (в), який повторюється з частотою ![]()
Із спектральних діаграм видно, що відстань між двома сусідніми гармоніками по осі частот (тобто відстань між вертикальними лініями) дорівнює значенню частоти повторення w0 періодичного сигналу. Це означає, що зі збільшенням частоти w0 повторення або зменшенням періоду Т0 сигналу відстань між вертикальними лініями на спектральних діаграмах збільшується (спектр стає рідшим, але займає ширший діапазон частот) і навпаки. Крім того, як випливає з виразів (1.5) – (1.7), зміна частоти повторення (або періоду) сигналу впливає також і на величину амплітуд гармонік.
Згадану властивість спектра періодичного сигналу зручно використати під час визначення спектрів імпульсних сигналів, які не є періодичними.
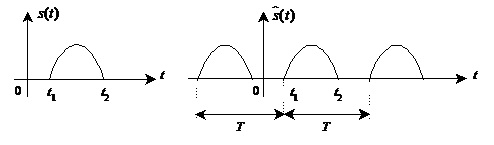
Приймемо, що імпульсний сигнал s(t) має форму поодинокого імпульсу (рис.1.3, а), який відрізняється від нуля на часовому проміжку (t1, t2).
|
а |
б |
Рис.1.3. До спектрального аналізу імпульсного сигналу
Імпульсний (поодинокий) сигнал як граничний випадок періодичного сигналу при Т®¥.
Перетворимо заданий
поодинокий імпульс на періодичний сигнал ![]() повторенням
його з довільним періодом T>(t2-t1), як показано на рис.1.3, б. Отриману періодичну
функцію
повторенням
його з довільним періодом T>(t2-t1), як показано на рис.1.3, б. Отриману періодичну
функцію ![]() розкладемо
в ряд Фур’є, причому коефіцієнти А0,
Ак, Ск, Sк
будуть тим меншими, чим більшим буде вибрано інтервал Т як період. Це випливає з виразів (1.5) – (1.7). Якщо період Т збільшувати до нескінченності, то всі
імпульси, крім первинного, змістяться у нескінченність і залишиться лише
первинний імпульс s(t).
розкладемо
в ряд Фур’є, причому коефіцієнти А0,
Ак, Ск, Sк
будуть тим меншими, чим більшим буде вибрано інтервал Т як період. Це випливає з виразів (1.5) – (1.7). Якщо період Т збільшувати до нескінченності, то всі
імпульси, крім первинного, змістяться у нескінченність і залишиться лише
первинний імпульс s(t).
Отже,
![]() (1.10)
(1.10)
При тому одержимо нескінченно малі амплітуди гармонічних складових, сума яких дає початкову неперіодичну функцію s(t), задану в інтервалі (t1, t2).
Оскільки при Т®¥ основна частота функції w0=(2p/Т) ®0, то це означає, що відстань по осі частот між спектральними лініями на спектральних діаграмах (яка дорівнює основній частоті w0) стає нескінченно малою, а спектр – суцільним. Отже, доходимо висновку, що при спектральному поданні імпульсних неперіодичних сигналів отримуємо суцільний спектр, який складається з нескінченно великої кількості гармонічних коливань з нескінченно малими амплітудами, частота яких неперервно змінюється від нуля до нескінченності.
Опишемо сказане
математично. Амплітуди косинусних та
синусних складових к-ї гармоніки
періодичного сигналу ![]() записуємо
виразами:
записуємо
виразами:
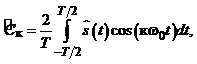 (1.11)
(1.11)
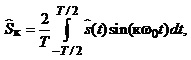 (1.12)
(1.12)
де w0=2p/Т.
Якщо Т зростає до нескінченності, то частота w0 прямуватиме до нуля, і її необхідно замінити нескінченно малою величиною dw. Крім того, добуток кw0 може набувати довільних значень і стане неперервною (а не дискретною) функцією к, тому величину кw0 необхідно розглядати як неперервну змінну частоту w, яка змінюється від нуля до нескінченності.
Враховуючи це, отримуємо вирази для малих амплітуд косинусних та синусних складових:
Косинус - перетворення та синус - перетворення Фур’є – складові спектральної характеристики імпульсних сигналів.
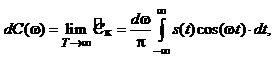 (1.13)
(1.13)
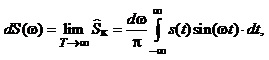 (1.14)
(1.14)
Введемо позначення:
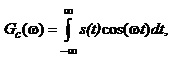 (1.15)
(1.15)
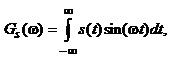 (1.16)
(1.16)
Формули (1.15) та (1.16) називають відповідно косинус-перетворенням Фур’є та синус-перетворенням Фур’є.
Результуючі амплітуди складових спектра на довільній частоті w дорівнюють:
![]() (1.17)
(1.17)
а їхні початкові фази:
Спектральна густина – основна спектральна характеристика імпульсних сигналів.
![]() (1.18)
(1.18) ![]() (1.19)
(1.19)
Функцію G(w) називаюь модулем спектральної густини, що описує амплітудний спектр імпульсного сигналу, а функцію y(t), яка описує фазовий спектр цього сигналу, називають аргументом спектральної густини.
Зауважимо, що спектральна густина – не спектр, а лише спектральна характеристика імпульсного сигналу, оскільки на конкретній частоті амплітуда відповідної спектральної складової дорівнює нулеві.
Отже, імпульсний (неперіодичний) сигнал – це сукупність нескінченної кількості гармонічних складових із нескінченно малими амплітудами dA(w), початковими фазами y(w), частота яких неперервно змінюється від нуля до нескінченності, що математично можна записати так:
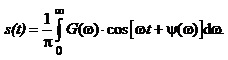 (1.20)
(1.20)
4. Часовий (динамічний) опис сигналів
Часовий (динамічний) опис сигналів
Як елементарні сигнали у часовому описі складних сигналів використовують одиничний стрибок та дельта-імпульс.
Одиничний стрибок (функція Хевісайда) загалом задається виразом:
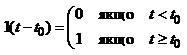 (1.21)
(1.21)
Функція Хевісайда як елементарний сигнал.
Застосування
одиничного стрибка для математичного опису аналогових сигналів полягає в тому,
що спочатку замінюють (апроксимують) аналоговий сигнал s(t) ступінчатим сигналом 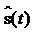 , який утворюється як сума вписаних у сигнал s(t)
та зміщених на Dt
елементарних стрибкоподібних сигналів, амплітуди яких пропорційні до деяких
вагових коефіцієнтів Dsk (див. рис. 1.4).
, який утворюється як сума вписаних у сигнал s(t)
та зміщених на Dt
елементарних стрибкоподібних сигналів, амплітуди яких пропорційні до деяких
вагових коефіцієнтів Dsk (див. рис. 1.4).
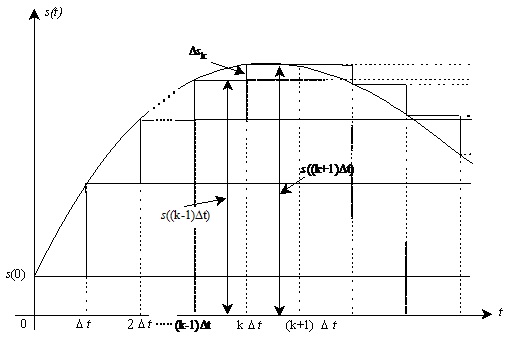
Рис.1.4. Заміна аналогового сигналу
ступінчатим
Часовий опис сигналів як послідовності стрибкоподібних змін.
Як видно з рис. 1.4, значення вагових коефіцієнтів Dsk у моменти часу tk=kDt дорівнюють різниці відліків сигналу s(t) у поточний і попередній моменти часу:
Dsk=s(tk)- s(tk-1)=s(kDt)-s((k-1) Dt)
Поточне значення сигналу s(t) у довільний момент t£NDt наближено описує вираз:
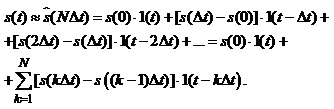 (1.22)
(1.22)
Похибка апроксимації
сигналу s(t) ступінчастим сигналом 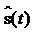 буде
зменшуватись зі зменшенням інтервалу Dt і у граничному випадку (Dt->0) сигнали s(t)
та
буде
зменшуватись зі зменшенням інтервалу Dt і у граничному випадку (Dt->0) сигнали s(t)
та 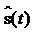 будуть
збігатися. У такому разі динамічну модель аналогового сигналу s(t), поданого
через функції Хевісайда, отримуємо із (1.22) заміною дискретної змінної kDt неперервною змінною t, малих приростів [s(kDt)-s((k-1)Dt)] – диференціалом
будуть
збігатися. У такому разі динамічну модель аналогового сигналу s(t), поданого
через функції Хевісайда, отримуємо із (1.22) заміною дискретної змінної kDt неперервною змінною t, малих приростів [s(kDt)-s((k-1)Dt)] – диференціалом ![]() , знака суми – інтегралом:
, знака суми – інтегралом:
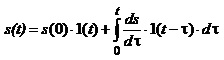 (1.23)
(1.23)
Інший спосіб математичного опису аналогового сигналу ґрунтується на використанні дельта-імпульсу (функції Дірака), який в загальному випадку задається виразом:
Функція Дірака як елементарний сигнал.
 (1.24)
(1.24)
Дельта-імпульс є імпульсом нескінченно короткої тривалості з нескінченно великою амплітудою та площею, що дорівнює одиниці, тобто
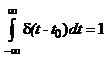 (1.25)
(1.25)
Функція Дірака є похідною від функції Хевісайда, а функція Хевісайда – інтегралом від функції Дірака:
![]() (1.26)
(1.26)
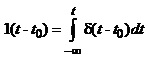 (1.27)
(1.27)
Використовуючи
дельта-імпульс, аналоговий сигнал s(t) апроксимують сигналом 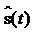 , що утворений зміщеними в часі на інтервали Dt прямокутними імпульсами заввишки sk=s(tk)=s(kDt) та
тривалістю Dt, як показано на рис.1.5
, що утворений зміщеними в часі на інтервали Dt прямокутними імпульсами заввишки sk=s(tk)=s(kDt) та
тривалістю Dt, як показано на рис.1.5
Часовий опис сигналів як послідовності прямокутних імпульсів.
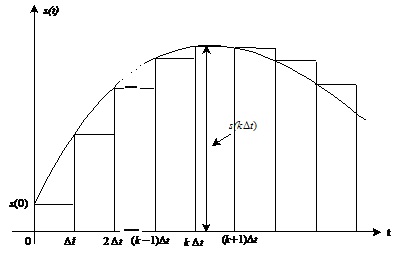
Рис.1.5. Апроксимація аналогового сигналу послідовністю прямокутних імпульсів
Розглядаючи кожний елементарний імпульс як різницю двох стрибків, зсунутих у часі один відносно одного на інтервал Dt, можемо наближено записати поточне значення сигналу s(kDt) в інтервалі kDt£t<(k+1)Dt у вигляді:
а для сигналу загалом:
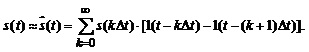 (1.28)
(1.28)
Похибка апроксимації
s(t) сигналом 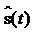 буде
зменшуватися у разі зменшення інтервалу Dt. У граничному випадку (Dt->0), замінюючи у (1.28) дискретну змінну kDt неперервною змінною t, знак суми – інтегралом, та враховуючи
(1.26), отримуємо динамічну модель аналогового сигналу з використанням
дельта-функції:
буде
зменшуватися у разі зменшення інтервалу Dt. У граничному випадку (Dt->0), замінюючи у (1.28) дискретну змінну kDt неперервною змінною t, знак суми – інтегралом, та враховуючи
(1.26), отримуємо динамічну модель аналогового сигналу з використанням
дельта-функції:
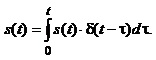 (1.29)
(1.29)
Примітка: для одержання формули (1.29) використано співвідношення:
На закінчення зауважимо, що подання складного сигналу сукупністю елементарних однотипних сигналів дає змогу застосувати для аналізу електричних кіл принцип накладання (суперпозиції), згідно з яким реакція лінійного електричного кола на дію цього складного сигналу дорівнює сумі реакцій, викликаних кожним елементарним сигналом. Використання цього принципу істотно полегшує аналіз електричних кіл і є основою багатьох поширених методів аналізу.
5. Операторний опис сигналів
5. Операторний опис сигналів
Перетворення Лапласа як узагальнення перетворення Фур’є.
Вище зазначалось, що спектральний опис сигналу s(t) можливий, якщо він задовольняє умову абсолютної інтегрованості. Проте чимало важливих сигналів, таких, як одиничний стрибок, гармонічне коливання та багато інших, не задовольняють цієї умови, і тому для них не можна отримати спектрального опису на підставі перетворення Фур’є. Для спектрального подання таких сигналів можна застосувати перетворення Лапласа, яке є узагальненням перетворення Фур’є і ґрунтується на використанні поняття комплексної частоти. Річ у тім, що при перетворенні Фур’є сигнал описують у вигляді суми нескінченної кількості елементарних гармонічних складових, кожна з яких змінюється у часі за законом exp(jwt).
Примітка: нагадаємо, що згідно з відомою формулою Ейлера гармонічне коливання можна подати сумою двох експонент з уявними показниками:
cos(wt)=[exp(jwt)+exp(-jwt)]/2,
sin(wt)=[exp(jwt)-exp(-jwt)]/2j.
Зображення Лапласа дає змогу отримати спектральний опис сигналів, визначених при t³0, які не задовольняють умову абсолютної інтегрованості.
Узагальнення перетворення Фур’є полягає в тому, що замість експоненційних сигналів з уявними показниками jw застосовують експоненційні сигнали з комплексними показниками exp(pt), де p=s+jw – комплексне число, яке прийнято називати комплексною частотою.
Використання поняття комплексної частоти дає змогу отримати спектральний опис сигналів, математичні моделі яких не задовольняють умову абсолютної інтегрованості. Ці сигнали повинні бути визначені при t³0, а при від’ємних значеннях t – дорівнювати нулеві. Перетворення Лапласа для таких сигналів описують виразом:
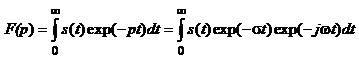 (1.30)
(1.30)
Зауважимо, що цей інтеграл існує завдяки тому, що функція s(t)×exp(-st) задовольняє умову абсолютної інтегрованості при t>0, а з іншого боку, тому, що при t<0 функція s(t)=0 (у протилежному випадку множник exp(-st) міг би призвести до розходження інтеграла).
Сигнал s(t) називають оригіналом, а функцію F(p) – зображенням оригіналу за Лапласом (або зображенням Лапласа).
Не наводячи доведення, зазначимо, що маючи зображення F(p), можна знайти оригінал s(t) на підставі формули:
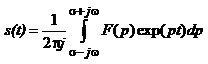 (1.31)
(1.31)
Інтегрування в площині комплексної змінної р здійснюється уздовж нескінченної вертикальної лінії, розміщеної з правого боку від уявної осі на відстані s. Детальніше це питання розглянуто в теорії функцій комплексної змінної.
Формули (1.30) та (1.31) називають відповідно прямим та зворотним перетворенням Лапласа.
На практиці для знаходження оригіналів та зображень сигналів широко використовують таблиці, в яких наведено зображення за Лапласом для значної кількості оригіналів.
Взаємну відповідність між оригіналом s(t) та його зображенням F(p) за Лапласом позначимо: s(t)¸F(p).
Для прикладу наведемо таблицю зображень Лапласа для деяких поширених сигналів.
Таблиця 1.1
|
Оригінал s(t) |
Зображення F(p) |
|
|
1 |
Множення сигналу на константу: A×s(t) |
A×F(p) |
|
2 |
Диференціювання
сигналу: |
p×F(p)-s(0) |
|
3 |
Інтегрування сигналу: |
F(p)/p |
|
4 |
Зсув сигналу в часі: s(t-t0) |
F(p)exp(-pt0) |
|
5 |
Одиничний стрибок: 1(t) |
1/p |
|
6 |
Дельта-імпульс: d(t) |
1 |
|
7 |
Гармонічні коливання (якщо t³0) cos(wt) sin(wt) |
p/(p2+w2) w/(p2+w2) |
|
8 |
Експоненційні сигнали (якщо t³0): e±at |
1/p(p+a) |
На закінчення зауважимо, що між зображенням Лапласа та спектральною функцією сигналу існує такий взаємозв’язок: якщо у виразі для зображення Лапласа замість р підставити jw, то отримуємо спектральну функцію цього сигналу.
Заміною р=jw у зображенні Лапласа отримуємо спектральну функцію G(jw) сигналу s(t).
Операторний опис сигналів знайшов широко застосовується в аналізі процесів у лінійних електричних колах, оскільки він дає змогу звести диференціальні рівняння кола до алгебричних, записаних відносно операторних зображень сигналів, що істотно спрощує знаходження розв’язку в операторній формі. Перехід від зображення шуканого сигналу до оригіналу здійснюють, як правило, на підставі таблиць операторних зображень.
6. Дискретизовані та цифрові сигнали
Особливістю розглянутих раніше аналогових сигналів є те, що сукупність їхніх миттєвих значень на довільному часовому інтервалі описується неперервною (нескінченною) множиною точок, кожна з яких відображає миттєве значення сигналу у відповідний момент часу і може набувати неперервну (нескінченну) множину значень. Отже, уся множина точок містить у собі нескінченну кількість інформації, тому вона часто малопридатна для сприйняття, аналізу та ефективного оброблення і потребує стискання первинної інформації без істотної втрати корисної інформації.
Дискретизація – подання сигналу скінченною множиною миттєвих значень.
Перетворення аналогового сигналу в дискретний у часі чи цифровий сигнал еквівалентне поданню його скінченною множиною точок, що полегшує зберігання та оброблення інформації, дає змогу збільшувати кількість сигналів, які поширюються по одному й тому самому каналу зв’язку (ущільнювати канали зв’язку), стискати первинну інформацію тощо.
Дискретизацією називають таке перетворення аналогового сигналу s(t), за якого його описують множиною миттєвих значень s(ti) у фіксовані моменти часу t1, t2, ...tn (рис.1.6)
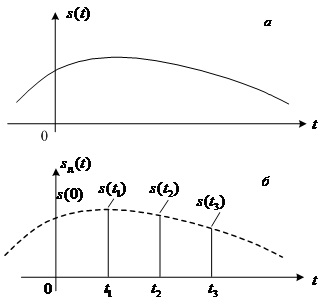
Рис.1.6. Дискретизація аналогового сигналу
Миттєві значення s(ti) дискретизованого сигналу називають відліками, а часовий інтервал Dt= ti-ti-1=T0 між двома сусідніми відліками – інтервалом дискретизації. Очевидно, що збільшення інтервалу дискретизації збільшує пропускну здатність каналу зв’язку, але одночасно збільшує і похибку відтворення первинного сигналу s(t). Тому інтервали дискретизації вибирають з урахуванням того, щоб на підставі наявних відліків s(ti) можна відтворити із заданою точністю первинну функцію s(t) на приймальному пункті.
Здебільшого для сигналів, які утворюються у джерелах інформації, характерні порівняно повільні зміни в часі миттєвих значень та велика тривалість. Аналіз спектральних властивостей таких сигналів показує, що їхній спектральний склад здебільшого зосереджується в обмеженій смузі частот 0...wв, а спектральні складові з частотами, вищими від wв, практично відсутні. Такі сигнали прийнято називати сигналами з обмеженим спектром. Саме ця властивість дає змогу замінити, а відтак знову відновити із заданою точністю неперервний сигнал, заданий скінченною множиною відліків, узятих у дискретні моменти часу.
Умови вибору інтервалу дискретизації сигналу з обмеженим спектром визначає теорема відліків (теорема Котельникова – Шеннона).
Умови вибору інтервалу дискретизації Dt, який забезпечує відновлення із заданою точністю первинного аналогового сигналу s(t), формулює теорема відліків (теорема Котельникова – Шеннона): неперервний сигнал s(t), у спектрі якого відсутні частоти, вищі від wв, повністю визначається послідовністю своїх миттєвих значень, узятих через інтервал часу Dt£p/wв, і може бути поданий рядом:
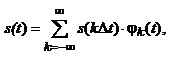 (1.32)
(1.32)
в якому базисні функції мають вигляд:
jk(t)=sin[wв(t-kDt)]/[wв(t-kDt)] (1.33)
Ряд (1.32) відомий як ряд Котельникова. Він дає змогу визначити первинний сигнал у довільний момент часу на підставі відліків його миттєвих значень, які слугують ваговими коефіцієнтами при базисних функціях.
Базисні функції мають таку властивість:
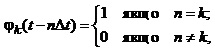
де n – ціле додатне або від’ємне число.
На
рис.1.7 зображено графіки базисних функцій для різних значень k, звідки бачимо,
що кожна базисна функція jk(t) зсунута
стосовно найближчої сусідньої функції jk-1(t) або jk+1(t) на час ![]() , який
відповідає інтервалові дискретизації Dt .
, який
відповідає інтервалові дискретизації Dt .
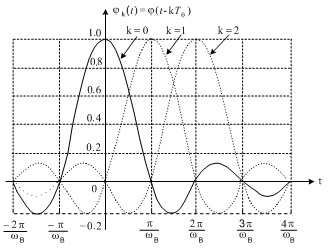
Рис.1.7. Графіки базисних функцій j(t-kT0)
Відновлення аналогового сигналу s(t) на підставі ряду (1.32) зображено на рис.1.8, звідки бачимо, що точні значення сигналу s(t) отримуємо в точках відліку ....-2T0, - T0, 0, T0, 2T0 і т.д. Між точками відліку сигнал визначається точно лише тоді, коли додаються усі члени ряду, кількість яких нескінченно велика.
Точне відновлення аналогового сигналу можливе лише за умови урахування нескінченної кількості відліків.
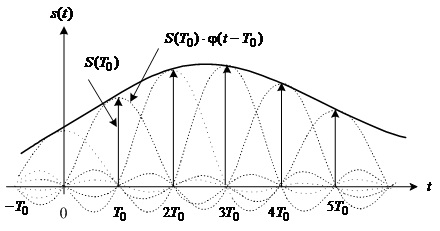
Рис.1.8. Відновлення аналогового сигналу на підставі послідовності відліків
Математична модель дискретизованого сигналу вимагає використання функції Дірака (d-функції).
Якщо неперервний в часі сигнал s(t) з найвищою частотою спектра wв подати через ряд (1.32) на деякому обмеженому інтервалі Тс, то кількість відліків N дорівнюватиме: N=Tc/Dt=Tcwв/p. Цю кількість відліків називають кількістю ступенів свободи сигналу s(t), або базою сигналу. У такому разі сигнал наближено описують рядом, який складається із скінченної кількості членів, і він відтворюється точно лише в точках відліку kDt. У проміжках між відліками з’являється похибка апроксимації, яка збільшується біля країв інтервалу Тс, де відкинуті члени ряду мають найбільше значення.
Математичну модель
дискретизоваого сигналу можна подати у вигляді добутку первинного неперервного
аналогового сигналу s(t) і періодичної послідовності ![]() -імпульсів:
-імпульсів:
Правильний вибір частоти дискретизації забезпечує відтворення первинного сигналу за допомогою фільтра нижніх частот.
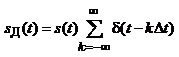 . (1.34)
. (1.34)
Для спектрального
опису дискретизованого сигналу ![]() застосовують до функції (1.34) пряме
перетворення Фур’є.
застосовують до функції (1.34) пряме
перетворення Фур’є.
Пропускаючи відповідні математичні викладки, зазначимо, що модуль спектральної функції Gд(w) дискретизованого сигналу sд(t) має вигляд модуля спектральної функції G(w) первинного неперервного аналогового сигналу і повторюється з частотою дискретизації w0=2p/Dt=2wв. Формування модуля спектральної функції Gд(w) дискретизованого сигналу показано на рис.1.9.
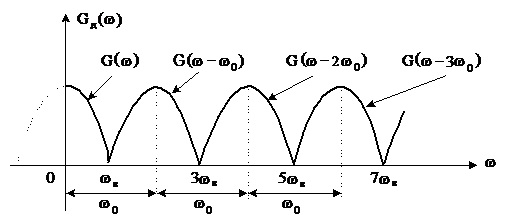
Рис.1.9. Модуль спектральної функції Gд(w) дискретизованого сигналу
На практиці частоту дискретизації wД вибирають дещо вищою, ніж 2wв (тобто Dt<p/wв), оскільки у такому разі сусідні спектри не перекриваються між собою, що випливає із рис.1.9. Тоді можна відтворити первинний сигнал із дискретизованого, виділивши перший пелюсток спектра за допомогою фільтра нижніх частот.
Практично важливим є питання спектрального опису дискретизованого сигналу sд(t), який заданий на часовому інтервалі [0, Тс] своїми відліками s(0), s(Dt), s(2Dt), ...s((N-1)Dt). Загальна кількість відліків дорівнює N=Tc/Dt. Спектральний опис такого сигналу ґрунтується на припущенні, що сигнал sд(t) є періодичним з періодом Тс, тому застосовують його розклад у ряд Фур’є і знаходять відповідні амплітудні коефіцієнти.
Спектральний опис дискретизованого сигналу ґрунтується на припущенні про періодичність цього сигналу.
Часовий опис дискретизованого сигналу має вигляд:
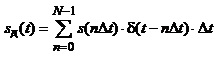 (1.35)
(1.35)
Комплексний ряд Фур’є такого сигналу описує формула:
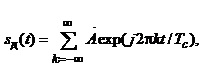 (1.36)
(1.36)
де комплексні амплітуди визначаємо за формулою:
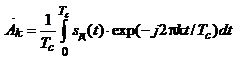 (1.37)
(1.37)
Підставивши вираз (1.35) в (1.37) та враховуючи фільтрувальну властивість дельта-імпульсу, отримуємо:
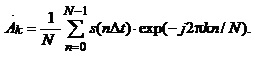 (1.38)
(1.38)
Формулу (1.38) називають дискретним перетворенням Фур’є (ДПФ) розглянутого сигналу. Вона визначає сукупність коефіцієнтів ряду Фур’є, які утворюють спектр дискретизованого сигналу.
Кількість відліків дискретизованого сигналу дорівнює подвоєній кількості гармонічних складових, які можна визначити на підставі ДПФ.
Аналіз властивостей ДПФ показує, що кількість різних комплексних амплітуд (крім постійної складової), які можна визначити за формулою (1.38), дорівнює половині кількості відліків за період Тс,тобто N/2.
Постійна
складова дискретизованого сигналу дорівнює середньому арифметичному усіх
відліків сигналу: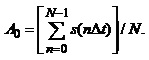
Часто розглядають
зворотну задачу дискретного спектрального аналізу: за відомими коефіцієнтами ![]() ДПФ треба
визначити відліки дискретизованого сигналу.
ДПФ треба
визначити відліки дискретизованого сигналу.
Для цього у формулі (1.36) приймають t=nDt і підсумовують скінченну кількість членів ряду, які відповідають гармонікам, що входять до ряду.
Отже, відліки дискретизованого сигналу визначають за формулою:
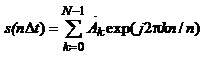 (1.39)
(1.39)
яка описує зворотне (обернене) дискретне перетворення Фур’є.
Цифрові сигнали подають у вигляді n-розрядних двійкових чисел.
Дискретні перетворення Фур’є широко застосовують, використовуючи цифрові сигнали для подання та оброблення різноманітної інформації.
Цифрові сигнали – це дискретизовані у часі та квантовані за рівнем сигнали. Кожен з рівнів подається, як правило, у вигляді n - розрядного двійкового числа:
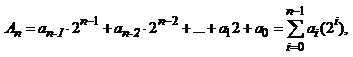 (1.40)
(1.40)
Електричний цифровий сигнал можна сформувати за принципом “додатної” або “від’ємної” логіки у вигляді паралельного або послідовного коду.
де аі – цифра в і-му розряді двійкового числа, яка може набувати значення 0 або 1.
Множник 2і відіграє роль вагового коефіцієнта. Отже, двійкові числа подають у вигляді комбінацій нулів та одиниць, які відповідають значенням цифр у відповідних розрядах.
В електричному цифровому сигналі роль “нулів” та “одиниць” відіграють звичайно сигнали напруги, які можуть бути сформовані за двома принципами:
а) додатної логіки – коли логічній “одиниці” відповідає високе значення потенціалу, а логічному “нулеві” – низьке;
б) від’ємної логіки – коли логічній “одиниці” відповідає низьке значення потенціалу, а логічному “нулеві” – високе.
Значення потенціалів, що відповідають “нулеві” та одиниці”, називають стандартними значеннями логічних сигналів.
Із сказаного випливає, що цифровий сигнал – це послідовність комбінацій стандартних значень логічних сигналів, які утворюють n-розрядний цифровий код. Зауважимо, що стандартні сигнали відповідних розрядів можуть з’являтись одночасно (паралельний код) або послідовно (послідовний код).
Найпоширеніший спосіб перетворення аналогового сигналу на цифровий полягає у дискретизації аналогового сигналу в часі та у квантуванні відліків за рівнем. Питання дискретизації аналогових сигналів розглянуто раніше, тому далі коротко зупинимось на особливостях квантування за рівнем.
При квантуванні сигналу за рівнем неперервна множина значень аналогового сигналу s(t) замінюється множиною дискретних значень. Враховуючи це, вибирають у заданому діапазоні значень smin...smax скінченну кількість дискретних значень (дискретних рівнів) і в моменти відліків tk=kDt значення сигналу s(kDt) замінюється найближчим дискретним значенням, як показано на рис.1.10.

|
а |
б |
в |
Рис.1.10. Формування цифрового сигналу
Відстань Ds між сусідніми дискретними рівнями
називають кроком квантування.
Загальна кількість дискретних рівнів у заданому діапазоні значень сигналу
дорівнює: ![]() . Оскільки кожному значенню дискретного рівня
ставиться у відповідність певний n-розрядний
двійковий код, то кількість необхідних розрядів визначають за формулою:
. Оскільки кожному значенню дискретного рівня
ставиться у відповідність певний n-розрядний
двійковий код, то кількість необхідних розрядів визначають за формулою:
n ≥ log2M (або 2n≥M) (1.41)
Кількість розрядів двійкового коду визначає кількість кроків квантування.
Найчастіше двійковий код відображає двійковий номер дискретного рівня.
Оскільки при квантуванні миттєве значення сигналу замінюється найближчим значенням дискретного рівня, то з’являється методична (систематична) похибка, яку прийнято називати шумом квантування. Очевидно, що похибка квантування має випадковий характер, її абсолютне значення у будь-який момент часу дорівнює різниці між квантованим значенням sкв(t) та миттєвим значенням сигналу s(t) і не перевищує половини кроку квантування.
Наявність шуму квантування – особливість процесу квантування.
Наявність методичної похибки означає, що істотною відмінністю квантування за рівнем від дискретизації у часі є те, що після реалізації квантування аналоговий сигнал не можна відновити з похибкою, меншою, ніж половина кроку квантування.
7. Модульовані сигнали та їх застосування
Як зазначалось вище, високочастотні коливання, які можна ефективно випромінювати, і які здатні поширюватись з малими втратами по каналу зв’язку, виконують роль переносника інформаційних сигналів, і відповідають певним повідомленням. Ці високочастотні коливання називають несучими або носійними.
Несуче коливання характеризується відповідними параметрами (амплітудою, частотою тощо), які визначають його форму та характер змін в часі. За відсутності інформаційного сигналу ці параметри є незмінними.
Як несучі коливання звичайно використовують періодичні коливання (неперервні або періодичну послідовність імпульсів), які мають дискретний (лінійчастий) спектр.
Найпростішим неперервним несучим коливання є гармонічне коливання:
Несуче високо-частотне коливання виконує роль переносника інформаційних сигналів.
![]() , (1.42)
, (1.42)
яке характеризується трьома параметрами: амплітудою Аm, частотою w0 та початковою фазою j0.
Найпростіший імпульсний переносник – періодична послідовність імпульсів прямокутної форми (рис.1.11), яка характеризується більшою кількістю параметрів:
амплітудою Аm, тривалістю імпульсів tі, періодом повторення Тn, а також іншими параметрами форми імпульсу.
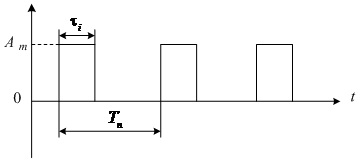
Рис.1.11. Імпульсний переносник
Вид модуляції визначає параметр несучого коливання, який змінюється під дією інформаційного керуючого сигналу.
Залежно від того, який з параметрів переносника змінюється відповідно до інформаційного керуючого сигналу, розрізняють різні види модуляції.
Так, для гармонічного переносника можливі три основні види модуляції: амплітудна (АМ), частотна (ЧМ) та фазова (ФМ). У деяких випадках використовують комбінацію цих видів.
Для імпульсного переносника можливі такі види модуляції: амплітудно-імпульсна (АІМ), фазоімпульсна(ФІМ), широтноімпульсна (ШІМ), частотно-імпульсна (ЧІМ), кодоімпульсна (КІМ).
Далі коротко розглянемо математичні моделі (ММ) та основні параметри модульованих сигналів.
8. Амплітудно-модульовані сигнали
Математичну модель АМ-сигналу можна записати в загальному вигляді:
sАМ(t)=Am(t)cos(w0t+j0), (1.43)
де Am(t) – функція, яка описує закон зміни амплітуди неперервного несучого коливання в часі. Ця функція повинна бути повільною порівняно з cos(w0t+j0), так, що за час, протягом якого повна фаза (w0t+j0) зміниться на 2p, функцію Am(t) можна вважати сталою. Функцію Am(t) називають обгинаючою (обвідною) АМ-сигналу. Математично її описують виразом:
![]() (1.44)
(1.44)
Математична модель АМ-сигналу описує зміну амплітуди несучого коливання під дією інформаційного сигналу.
де Am0 – амплітуда немодульованого (несучого) коливання, яка входить у (1.42); k – коефіцієнт пропорційності; u(t) – модулюючий (керуючий) сигнал.
Із (1.44) бачимо, що обгинаюча АМ-сигналу змінюється пропорційно до модулюючого сигналу u(t) стосовно амплітуди несучого коливання.
Формування АМ-сигналу зображено на рис.1.12.
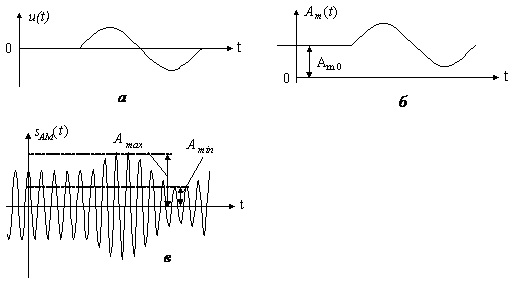
Рис.1.12. Формування АМ-сигналу: а – модулюючий сигнал;
б –- обгинаюча АМ-сигналу; в – АМ-сигнал
Забезпечення пропорційної залежності між обгинаючою АМ-сигналу та керуючим інформаційним сигналом – умова відсутності спотворень при амплітудній модуляції.
З урахуванням (1.44) математичну модель АМ-сигналу можна записати:
![]() (1.45)
(1.45)
звідки випливає, що між миттєвими значеннями модулюючого сигналу u(t) та обгинаючої Am(t) існує однозначний пропорційний зв’язок за умови:
![]() . (1.46)
. (1.46)
Якщо умова (1.46) не виконуєься, то форма обгинаючої Am(t) та модулюючого сигналу u(t) не збігаються – виникає небажане явище спотворення обгинаючої АМ-сигналу.
Основним параметром АМ-сигналу є коефіцієнт модуляції, який визначають як відношення максимального відхилення амплітуди модульованого сигналу стосовно амплітуди несучого (немодульованого) коливання до амплітуди несучого коливання:
![]()
Очевидно, що спотворення обгинаючої Am(t) АМ-сигналу відсутні, якщо виконується умова:
0<m<=1.
9. Сигнали з кутовою модуляцією (ЧМ- та ФМ-сигнали)
Термін “кутова модуляція” об’єднує частотну та фазову модуляцію, оскільки для неперервного несучого коливання (1.42) миттєві значення повної фази Y(t) та кутової частоти w(t) взаємопов’язані співвідношеннями:
![]() (1.47a)
(1.47a)
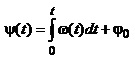 . (1.47б)
. (1.47б)
При кутовій модуляції керуючий інформаційний сигнал впливає одночасно на зміну частоти та повної фази несучого коливання.
Отже, параметри несучого коливання w та y не можуть змінюватись незалежно один від одного і вплив модулюючого сигналу на один із них викликає одночасну зміну другого. При кутовій модуляції амплітуда несучого коливання є сталою Am=const, а модулюючий сигнал керує повною фазою y (t).
Зауважимо, що за відсутності модуляції
повна фаза несучого (немодульованого) коливання змінюється в часі за лінійним
законом y(t)=w0t+j0 і згідно з (1.47а) кутова частота ![]() є сталою.
є сталою.
Можливі два варіанти кутової модуляції:
а) пропорційно до модулюючого сигналу u(t) змінюється миттєве значення частоти стосовно частоти несучого коливання w0:
wчм(t)=w0+кчмu(t), (1.48)
де kчм – коефіцієнт пропорційності.
Повна фаза yчм(t), згідно з (1.47б), змінюється стосовно лінійного закону пропорційно до інтеграла від модулюючого сигналу:
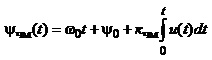 (1.49)
(1.49)
Такий варіант кутової модуляції називають частотною модуляцією.
Математична модель частотно-модульованих сигналів має вигляд:
Математична модель сигналу з кутовою модуляцією описує залежність повної фази несучого коливання від модулюючого інформаційного сигналу.
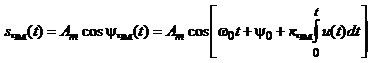 (1.50)
(1.50)
б) пропорційно до модулюючого сигналу змінюється повна фаза стосовно лінійного закону:
![]() (1.51)
(1.51)
При тому кутова частота не залишається сталою, а змінюється, згідно з (1.47а), пропорційно до похідної модулюючого сигналу стосовно частоти w0 несучого коливання:
![]() (1.52)
(1.52)
Цей варіант кутової модуляції називають фазовою модуляцією.
Математична модель фазомодульованого сигналу має вигляд:
![]() (1.53)
(1.53)
Основними параметрами сигналів з кутовою модуляцією є девіація частоти Dwmax та індекс модуляції М.
Девіація частоти – це максимальне відхилення частоти модульованого сигналу стосовно частоти несучого коливання w0.
На підставі (1.48) та (1.49) визначаємо девіацію частоти відповідно для ЧМ- та ФМ- сигналів:
![]() (1.54а)
(1.54а)
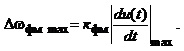 (1.54б)
(1.54б)
Індекс модуляції – це максимальне відхилення повної фази модульованого сигналу стосовно лінійного закону.
На підставі (1.49) та (1.51) визначаємо індекс модуляції відповідно для ЧМ- та ФМ сигналів:
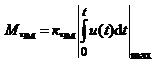 (1.55а)
(1.55а)
![]() (1.55б)
(1.55б)
Вимірюють девіацію частоти в рад/с або в герцах, а індекс модуляції – у радіанах або градусах.
10. Модуляція імпульсних коливань
Побудова математичної моделі модульованих сигналів з використанням високочастотного імпульсного переносника є достатньо складною і виходить за межі цього підручника, тому розглянемо лише часові діаграми сигналів за різних видів модуляції.
У разі АІМ імпульси змінюють амплітуду пропорційно до модулюючого сигналу, але зберігається незмінною їхня тривалість на період повторення (рис.1.13, б).
У разі ФІМ імпульси зберігають тривалість та амплітуду, проте моменти їхньої появи зміщуються у часі стосовно їхніх початкових значень на деяку величину Dt, яка пропорційна до миттєвого значення модулюючого сигналу. Часову діаграму для гармонічного модулюючого сигналу наведено на рис.1.13, в.
У разі ЧІМ імпульси зберігають незмінними тривалість та амплітуду, проте змінюється частота їхнього повторення пропорційно до миттєвих значень модулюючого сигналу (рис.1.13, г).
Вид імпульсної модуляції визначає параметр імпульсного переносника, який змінюється під дією модулюючого інформаційного сигналу.
У разі ШІМ змінюється тривалість імпульсів пропорційно до миттєвих значень модулюючого сигналу. Розрізняють односторонню ШІМ, коли один із фронтів імпульсу пересувається під час процесі модуляції, а другий зберігає своє розміщення у часі, та двосторонню – коли пересуваються обидва фронти симетрично стосовно середини імпульсу. Можливий вигляд послідовності імпульсів з односторонньою ШІМ при гармонічному модулюючому сигналі зображено на рис.1.13, д.
При кодоімпульсній модуляції керуючим сигналом є цифровий сигнал, який відповідає миттєвому значенню первинного модулюючого сигналу у двійковій системі числення.
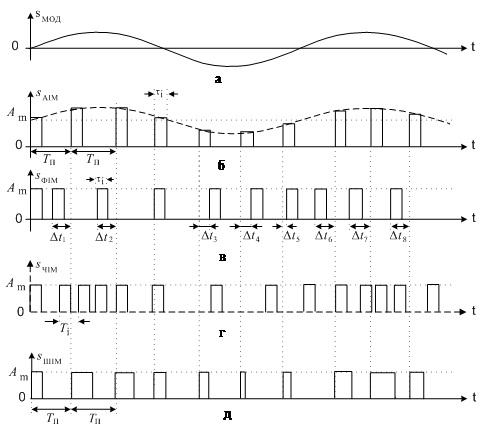
Рис.1.13. Часові діаграми: а – гармонічного модулюючого сигналу;
б – АІМ - сигналу; в – ФІМ - сигналу; г – ЧІМ - сигналу; д – ШІМ - сигналу
При КІМ імпульси зберігають тривалість та амплітуду, проте у фіксовані моменти часу, які визначені періодом повторення, з’являється не один імпульс, а “пакет” імпульсів, кодова послідовність яких відповідає у двійковій системі числення миттєвому значенню модулюючого сигналу в цей момент. Отже, сигнал з КІМ відповідає цифровому сигналові, у якого нулям та одиницям відповідає відсутність або наявність імпульсу у пакеті.
11. Стохастичні (випадкові) сигнали
Оскільки характер прийнятих сигналів як носіїв інформації на приймальному пункті заздалегідь не є відомим, то з цього погляду сигнали треба розглядати як випадкові функції часу.
Отже, математичною моделлю випадкового сигналу є випадкова функція часу.
Випадкова функція будь-якого аргументу – це така функція, значення якої для кожного значення аргументу випадкове. Випадкову функцію часу називають випадковим процесом. Позначимо його функцією X(t).
Спостерігаючи багаторазово за одним і тим самим випадковим процесом, що перебігає в незмінних умовах, кожен раз отримуємо конкретні реалізації x(t), не подібні одна на одну, проте на підставі такого спостереження можна виявити певні закономірності, що характеризують цей процес, та визначити сукупність невипадкових числових характеристик, які описують його. Випадковий процес повністю характеризується нескінченно великою кількістю реалізацій, які утворюють ансамбль реалізацій.
Ансамбль реалізацій випадкового процесу містить повну інформацію про закономірності, що характеризують цей процес.
Розглянемо N реалізацій випадкового процесу X(t) (рис.1.14).
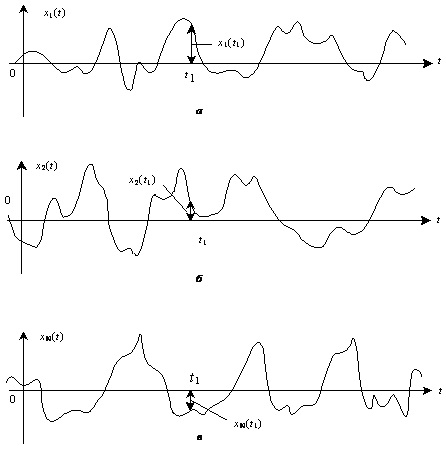
Рис.1.14. Ансамбль реалізацій випадкового процесу
Сукупність миттєвих значень випадкового процесу, заданого ансамблем реалізацій у довільний момент часу, називають перетином випадкового процесу.
На рис.1.14 показано перетин випадкового процесу X(t) у момент t1, який дає змогу визначити сукупність миттєвих значень процесу x1(t1), x2(t1), ...xN(t1), яку можна розглядати як сукупність значень деякої випадкової величини X(t1).
Ця сукупність дає можливість визначити одновимірну функцію розподілу ймовірностей випадкової величини X(t1). Для цього виділимо ті значення, які в момент часу t1 задовольняють умову:
X(t1)<x1, (1.56)
де x1 – деяке вибране значення випадкового процесу.
Позначимо кількість цих значень як n(x1, t1). Відношення n(x1, t1)/N називають у теорії ймовірностей частотою настання події. У такому разі під подією розуміємо виконання умови (1.56). За достатньо великого значення N відношення n(x1, t1)/N прямуватиме до постійного числа, яке називають ймовірністю того, що при t=t1 випадкова функція X(t) менша від значення x1:
Перетин випадкового процесу дає змогу визначити його одновимірну функцію розподілу та густину розподілу ймовірностей у довільний момент часу.
![]() (1.57)
(1.57)
Діючи аналогічно для інших значень x в інтервалі -¥ £ x £ ¥, можемо побудувати одновимірну функцію розподілу ймовірностей випадкового процесу:
F1(x, t1)=P{X(t1)<x}. (1.58)
Функція ![]() матиме
ступінчатий характер тоді, коли випадковий процес набуває дискретних значень.
Якщо ж випадковий процес змінює свої значення неперервно, то функція F1(x, t1) теж
матиме вигляд плавної кривої. Зауважимо, що функція розподілу ймовірностей є
неспадною функцією свого аргументу, що випливає з її означення.
матиме
ступінчатий характер тоді, коли випадковий процес набуває дискретних значень.
Якщо ж випадковий процес змінює свої значення неперервно, то функція F1(x, t1) теж
матиме вигляд плавної кривої. Зауважимо, що функція розподілу ймовірностей є
неспадною функцією свого аргументу, що випливає з її означення.
Тісно пов’язаною з одновимірною функцією розподілу ймовірностей випадкового процесу є одновимірна густина розподілу ймовірностей випадкового процесу, яку на підставі ансамблю реалізацій наближено визначають так:
![]() , (1.59)
, (1.59)
де n(x+Dx, t1) – кількість реалізацій, значення яких у момент t1 були менші від x+Dx, а n(x,t1) визначаємо, як і раніше.
За такого визначення густина розподілу теж має ступінчатий вигляд. Підвищення точності визначення густини розподілу досягають зменшенням інтервалу Dx до нуля:
![]() . (1.60)
. (1.60)
Із (1.60) випливає, що густина розподілу є похідною одновимірної функції розподілу:
![]() (1.61)
(1.61)
З іншого боку отримуємо:
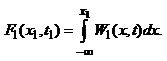 (1.62)
(1.62)
Очевидно, що ймовірність перебування випадкової функції X(t) у момент t1 в інтервалі між x1 та x2, дорівнює:
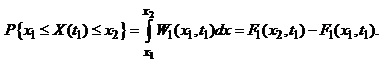 (1.63)
(1.63)
Зрозуміло, що ймовірність перебування значення випадкового процесу у межах від -¥ до ¥, дорівнює одиниці:
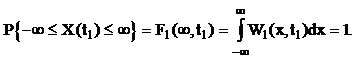 (1.64)
(1.64)
Інтегральний та диференціальний закони розподілу ймовірностей дають змогу визначити у довільний момент часу ймовірність перебування значення випадкової величини у заданих межах.
Зауважимо, що функції F1(x, t) та W1(x,t) для довільних значень x та t завжди набувають додатні значення.
Часто функцію розподілу ймовірностей F1(x,t) називають інтегральним законом розподілу, а густину розподілу ймовірностей – диференціальним законом розподілу ймовіростей.
Функції F1(x, t1) та W1(x,t1) статистично повністю характеризують значення випадкового процесу X(t) у заданий момент часу t1 і тому їх називають одновимірними. Ці функції є найпростішими характеристиками випадкового процесу, оскільки вони дають уявлення про процес лише в окремі фіксовані моменти часу.
12. Числові характеристики випадкових сигналів
Проходження сигналів в електронних колах супроводжується різноманітними перетвореннями їхніх характеристик. У випадкових сигналів можуть змінюватися закони їхнього розподілу, аналітичний розрахунок яких дуже складний. Проте виявляється, що значно простішим є розрахунок певних числових характеристик законів розподілу, які можна визначити на підставі нескладних експериментів. У багатьох випадках точність розрахунків, яку забезпечують згадані числові характеристики, цілком достатня для потреб практики. Такими числовими характеристиками є моменти випадкової величини. Вони є детермінованими числами.
Числові характеристики випадкових сигналів використовують в аналізі їхнього проходження через електронні кола.
Момент n-го порядку Mn(x) неперервної випадкової величини х визначають за формулою:
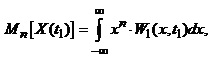 (1.65)
(1.65)
де W1(x,t1) – одновимірна густина розподілу ймовірностей випадкової величини x(t1).
Математичним сподіванням або середнім значенням випадкової величини називають момент першого порядку:
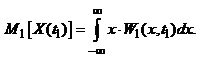 (1.66)
(1.66)
Усереднення випадкової величини x(t1) згідно з (1.66) здійснюють за ансамблем реалізацій. Тому за наявності ансамблю із N реалізацій випадкового процесу статистичне визначення його середнього значення у перетині в момент часу tk здійснюємо за формулою:
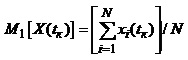 (1.67)
(1.67)
Взаємозв’язок між формою закону розподілу ймовірностей та його числовими характеристиками стає наочнішим у разі використання поняття центрованої випадкової величини. Випадкова величина називається центрованою, якщо її середнє значення дорівнює нулеві. Отже, випадкова величина X(tк) центрується відніманням від неї середнього значення M1[X(tк)]:
![]() . (1.68)
. (1.68)
Моменти випадкової величини є детермінованими числами, які визначають усередненням за ансамблем реалізацій в перетині у довільний момент часу.
На відміну від початкових моментів, які визначають за формулою (1.65), моменти центрованої величини називають центральними моментами. Центральний момент n-го порядку розраховують за формулою:
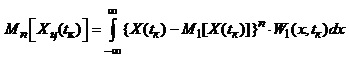 . (1.69)
. (1.69)
Центральний момент першого порядку M1[Xц(tk)] за означенням дорівнює нулеві.
Центральний момент другого порядку
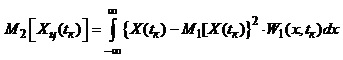 (1.70)
(1.70)
Цей момент характеризує розсіювання можливих значень випадкової величини X(tk) стосовно її середнього значення і називається дисперсією. Часто використовують таке позначення дисперсії:s2[X(tк)]. Величину s[X(tк)], що дорівнює додатному значенню кореня квадратного з центрального моменту другого порядку, називають середнім квадратичним відхиленням випадкової величини X(tк).
Арифметичним операціям над випадковими сигналами відповідають арифметичні операції над їхніми числовими характеристиками.
На підставі ансамблю з N реалізацій випадкового процесу статистичне визначення дисперсії виконуємо за формулою:
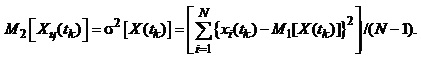 (1.71)
(1.71)
Розв’язуючи багато практичних задач, доводиться виконувати арифметичні операції над випадковими сигналами. При цьому числові характеристики результуючих сигналів достатньо просто визначають через числові характеристики первинних сигналів. Наприклад, якщо Х1(t) та Х2(t) є первинними незалежними сигналами, а А – постійна величина, то справедливі такі співвідношення:
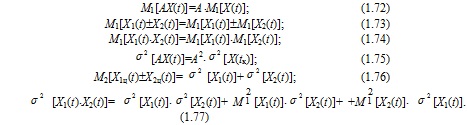
Подані співвідношення можна узагальнити для більшої кількості випадкових сигналів.
Загалом числові характеристики одновимірних розподілів залежать від часу. Це зумовлюється часовою залежністю функції розподілу F1(x,t) та густини розподілу W1(x,t). У такому разі числові характеристики замість чисел стають функціями часу і їх називають моментними функціями.
Точний опис випадкового сигналу забезпечують n-вимірна функція розподілу та n-вимірна густина розподілу ймовірностей, якщо n®¥.
Повніше можна описати випадковий процес, якщо визначити взаємозв’язок між його значеннями при двох і більше моментах часу. Такий взаємозв’язок описують n-вимірна функція розподілу ймовірностей Fn(x1, t1; x2, t2; ... xn, tn) та n-вимірна густина розподілу ймовірностей Wn(x1, t1; x2, t2; ...xn, tn). Очевидно, що чим більше значення n, тим точніше описуємо випадковий процес.
Зауважимо, що для великих значень n аналітичний опис функцій Fn (ּ) та Wn(ּ) дуже складний і практично дуже важко отримати його. Проте існують деякі типи випадкових процесів, властивості яких можна повністю описати за допомогою густини розподілу ймовірностей для скінченного значення n. Такими процесами є білий шум та марковські випадкові процеси.
Білий шум та марковський випадковий процес можна повністю описати за допомогою густини розподілу ймовірностей для скінченного значення n.
Білий шум характеризується тим, що його миттєві значення у різні моменти часу є незалежними. Отже, n -вимірну густину розподілу білого шуму повністю визначаємо добутком n одновимірних густин.
Марковські випадкові процеси характеризуються тим, що густина розподілу ймовірностей у момент ti залежить лише від значення випадкового процесу в попередній момент часу і не залежить від більш ранніх подій. Відповідний аналіз показує, що n-вимірну густину розподілу ймовірностей випадкового марковського процесу можна описати за допомогою густин розподілу ймовірностей, не вищих від другого порядку.
Закінчуючи розгляд основних характеристик випадкових сигналів, зазначимо, що множину випадкових процесів можна поділити на дві великі групи: стаціонарні та ергодичні.
Випадковий процес X(t) є стаціонарним, якщо будь-яка n-вимірна функція розподілу ймовірностей його значень, узятих у різні моменти часу, не змінюється за будь-якого зсуву (зміщення) цих моментів уздовж осі часу. Стаціонарні випадкові процеси виникають у джерелах випадкових сигналів за усталених режимів роботи, за незмінних умов зовнішнього середовища та незмінних значень параметрів електронних кіл, через які проходять випадкові сигнали.
Ергодичні випадкові процеси характерні тим, що їхні закони розподілу можна визначити, усереднюючи необхідні величини на підставі лише однієї реалізації, отриманої за достатньо великий проміжок часу. Це означає, що для ергодичних стаціонарних процесів усереднення за ансамблем реалізацій та усереднення в часі в межах одної реалізації дають однаковий результат.